Der Doppler Effekt
Contents
Voraussetzungen
mathematische Grundlagen der Fouriertransformation
Lerninhalte
Ausnutzung des Doppler Effekts zur Geschwindigkeitsmessung mithilfe der DFT
digitale Verarbeitung von Audiosignalen
Der Doppler Effekt¶
Hinweis
Der Inhalt dieser Seite lässt sich nicht interaktiv auf dieser Seite ausführen.
In dem folgenden Video ist kurz ein Verkehrsschild zu sehen: Hier ist eine Maximalgeschwindigkeit von 50 mph, bzw. ca. 80 km/h vorgeschrieben.
Eine Frage drängt sich nahezu auf: Hält sich der Fahrer des laut hupenden Autos an diese Geschwindigkeitsbegrenzung?
Eine weitere Sache fällt auf: Die Tonhöhe der Hupe ändert sich bei der Vorbeifahrt von einem hohen zu einem tiefen Ton. Dieses Phänomen wird als Doppler Effekt bezeichnet. Im Alltag macht er sich vor allem dann bemerkbar, wenn ein Krankenwagen oder ein Polizeiauto vorbeifährt und sich der Klang der Sirene ändert. In dem Moment, in dem das Fahrzeug vorbeifährt, klingt die Sirene plötzlich viel tiefer. Der Doppler Effekt ist auch die Ursache für den charakteristischen Klang von Rennautos, wenn sie an der Zuschauertribüne vorbeirasen.
Frequenzanalyse¶
Mit einem beliebigen Online Youtube-zu-mp3-Converter lässt sich die Tonspur des Videos extrahieren und mit der Funktion audioread in Matlab einlesen. Mit Hilfe der Signalverarbeitungstoolbox kann man sich dann ein Spektrogramm erstellen:
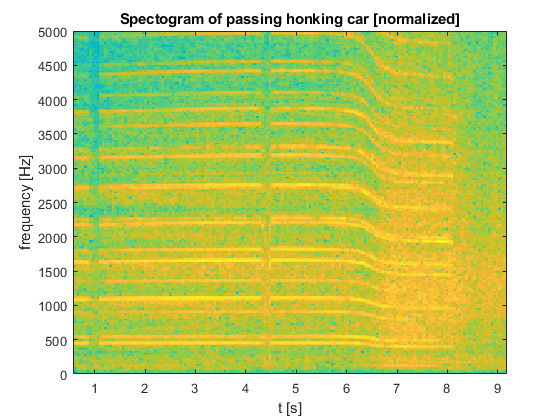
Auf der x-Achse ist die Zeit und auf der y-Achse die Frequenz aufgetragen. Die Farbe gibt eine Auskunft über die dominanten Frequenzen zu jedem Zeitpunkt. Zwischen Sekunde 6 und Sekunde 7 fährt das Auto an der Kamera vorbei und der Abfall in der Tonhöhe ist gut zu erkennen.
Die vielen horizontalen Linien sind ein Zeichen dafür, dass die Hupe des Fahrzeuges keinen reinen Sinuston erzeugt, sondern eine Überlagerung vieler Frequenzen ist. Eine sogenannte Fouriertransformation der Tonspur gibt uns Auskunft über die dominanten Frequenzen im gesamten Zeitfenster:
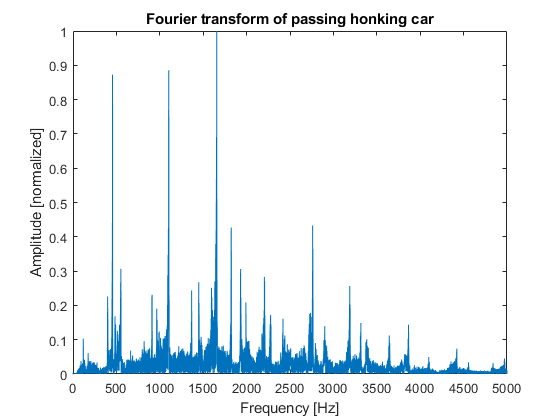
Für jede horizontale Linie im Spektrogramm erhalten wir einen Peak in der Fouriertransformation. Der Ton der Hupe ist also eine Überlagerung von hauptsächlich drei Tönen bzw. Frequenzen.
Die dominanteste Frequenz von 1658 Hz (dreigestrichenes gis) fällt beim Vorbeifahren auf 1449 Hz herab.
Die zweite Frequenz von 1104 Hz fällt beim Vorbeifahren auf 964 Hz ab.
Die dritte Frequenz von 456 Hz fällt herab auf 399 Hz.
Ursache des Dopplereffektes¶
Die Hupe des Fahrzeuges erzeugt einen Ton, oder mit anderen Worten, regt die umgebende Luft zum Schwingen an. Wenn diese Schwingungen auf unser Ohr treffen, nehmen wir sie als Ton wahr. Das Geräusch der Hupe breitet sich mit der Schallgeschwindigkeit von ca. 340 m/s im Raum aus.
Die Schallwellen breiten sich kreisförmig vom Auto aus. Wenn das Fahrzeug in Bewegung ist werden die Wellenberge vor dem Auto gestaucht und hinter dem Auto gestreckt, da es in eine Richtung den zuvor ausgesendeten Schallwellen hinterher fährt.
Die gestauchten Wellenberge vor dem Fahrzeug haben also eine höhere Frequenz als die gestreckten Wellenberge hinter dem Fahrzeug und werden deshalb auch als höherer Ton wahrgenommen.

Zurück zur ursprünglichen Fragestellung¶
Wie schnell fährt denn nun das Auto? Angenommen das Auto ruht und die Frequenz der Hupe beträgt \(f_A\). Das Signal breitet sich mit der Schallgeschwindigkeit von c = 340 m/s aus. Der Abstand zweier Wellenberge, also die Wellenlänge des Tons, ist dann
also genau die Distanz, die das Signal in der Zeit \(f_A^{-1}\) zurücklegt. Kommt das Auto auf uns zu verkürzt sich die Wellenlänge genau um die Strecke, die das Auto in der Zeit \(f_A^{-1}\) zurücklegt. Ist \(v\) die Geschwindigkeit des Autos, so verringert sich die Wellenlänge zu
Diese verringerte Wellenlänge wird vom Beobachter als höhere Frequenz \(f_{B,+}\) wahrgenommen:
Wenn wir die Originalfrequenz der Hupe kennen würden, könnten wir nun diese Gleichung nach \(v\) umstellen um die Geschwindigkeit zu bestimmen. Aus unserer vorangeschalteten Frequenzanalyse kennen wir aber nur die Frequenz \(f_{B,+}\) der Hupe, die wir wahrnehmen wenn das Auto auf uns zukommt und die Frequenz \(f_{B,-}\), die wir wahrnehmen, wenn das Auto sich wieder von uns entfernt.
Wir können die obigen Gleichungen aber für den Fall, dass das Auto sich von uns entfernt, genauso herleiten. In diesem Fall vergrößert sich die Wellenlänge genau um den Betrag, den das Auto in der Zeit \(f_A^{-1}\) zurücklegt:
was wir als tiefere Frequenz
wahrnehmen. Wenn wir nun die Gleichung für \(f_{B,+}\) durch die Gleichung für \(f_{B,-}\) teilen, kürzt sich die unbekannte Frequenz \(f_A\) raus:
Alle Werte in dieser Gleichung sind bekannt, bis auf \(v\). Wir können also nach \(v\) auflösen um die Geschwindigkeit des Autos aus den gemessenen Frequenzen zu bestimmen. Im Folgenden wird das für die drei identifizierten dominanten Frequenzen durchgeführt:
f1 = [1658, 1104, 456]; % frequencies approaching
f2 = [1449, 964, 399]; % frequencies retreating
c = 340; % speed of sound [m/s]
km_to_miles = 0.621371; % [miles/kilometer]
% f1/f2 = (c+v)/(c-v) =>
v = c*(f1 - f2)./(f1 + f2); %in [m/s]
v_kmh = v*3.6;
v_mph = v_kmh*km_to_miles
v_mph =
51.161 51.488 50.704
Die Toleranzen bei Geschwindigkeitsmessungen in USA liegen im Ermessen des Verkehrsbeamten, in der Regel geht man aber von ca. 5 mph aus. Glück gehabt!

 Github Repository
Github Repository