Github Repository
Lineare Interpolation
Voraussetzungen
mathematische Grundlagen der linearen Interpolation
Lerninhalte
Realisierung einer Routine zur linearen Interpolation
Lineare Interpolation¶
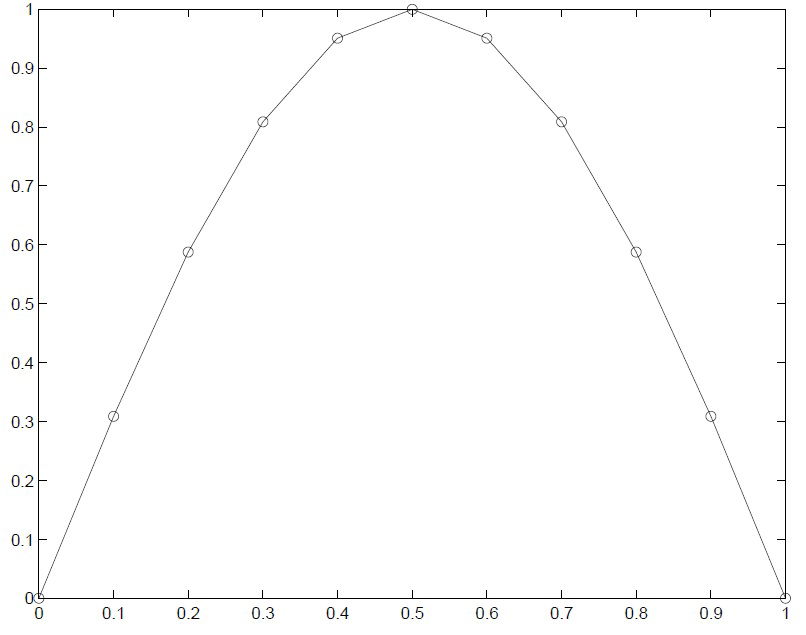
Gegeben seien die Messpunkte \((t_i; y_i)\), \(i = 1; ..; n\) eines Versuches. Dabei bezeichnet \(t_i\) einen Messzeitpunkt aus dem Intervall \([a; b]\) und \(y_i\) den dazugehörigen Messwert. Programmieren Sie eine Funktion, die für ein beliebiges \(t \in [a; b]\) einen Wert liefert, der auf der Verbindungslinie der benachbarten Messpunkte \((t_j ; y_j)\) und \((t_{j+1}; y_{j+1})\) liegt (lineare Interpolation).
Arbeiten Sie mit folgenden Angaben:
\(n = 11, [a; b] = [0; 1]\)
\(t_i\) |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
\(y_i\) |
0.00 |
0.31 |
0.59 |
0.81 |
0.95 |
1.00 |
0.95 |
0.81 |
0.59 |
0.31 |
0.00 |
Erstellen Sie dazu zunächst eine (gut dokumentierte) Funktion für die Interpolation:
%%file linint.m
function y=linint(t,tv,yv)
% Die Funktion linint interpoliert die in den Vektoren abgelegten Daten tv,yv linear.
% Dazu sollten die Daten in tv sortiert sein und ein t zwischen dem ersten
% und letzten Eintrag von tv eingegeben werden
%
% Eingabeparameter: tv, yv = Zeitpunkte und Messwerte,
% t = gewünschter Auswertezeitpunkt
% Ausgabeparameter: y = linear interpolierter Messwert zum Zeitpunkt t
%
%
… und dann ein Hauptprogramm, in welchem Sie die Funktion aufrufen und die Daten bereitstellen:
% zunächst werden zwei Vektoren tv und yv definiert,
% die alle Daten von t und y enthalten
%
tv=[ 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0];
yv=[ 0.00, 0.31, 0.59, 0.81, 0.95, 1.00, 0.95, 0.81, 0.59, 0.31, 0.00];
%
% Dann können sie Ihre Funktion linint testen, z.B. mit t=0.15
%
t=0.15;
y=linint(t,tv,yv)
Schreiben Sie das Programm nun so um, dass Sie die oben dargestellte Visualisierung erhalten.