Numerische Differentiation
Contents
Voraussetzungen
Programmier-Grundlagen
Lerninhalte
Grundlagen und Realisierung numerischer Differentiation
Herleitung von Differenzenquotienten
Bewertung von Genauigkeit und Aufwand von Differenzenquotienten
Numerische Differentiation¶
Um Ableitungen von Funktionen zu approximieren, die wir analytisch nicht berechnen können oder wollen, verwenden wir Differenzenquotienten. Im Wesentlichen unterscheiden wir zwischen
Vorwärtsdifferenzen, die für die Ableitung am Punkt x Funktionswerte größer als x mit einbeziehen, zum Beispiel \(f'(x) \approx \frac{f(x+dx) - f(x)}{dx}\),
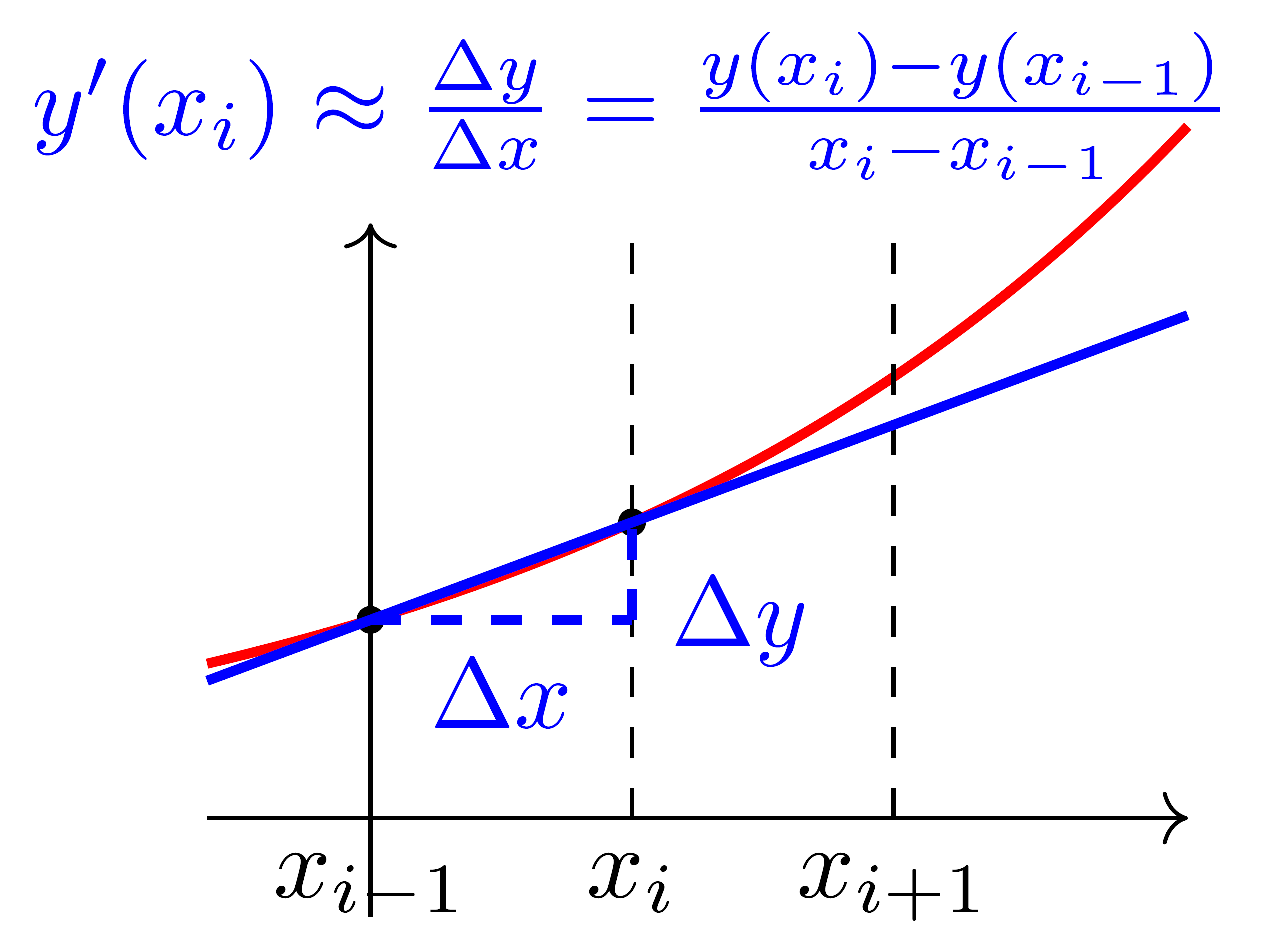
Zentrale Differenzen, die Funktionswerte größer und kleiner als x mit einbeziehen, zum Beispiel \(f'(x) \approx \frac{f(x+dx) - f(x-dx)}{2 dx}\), und
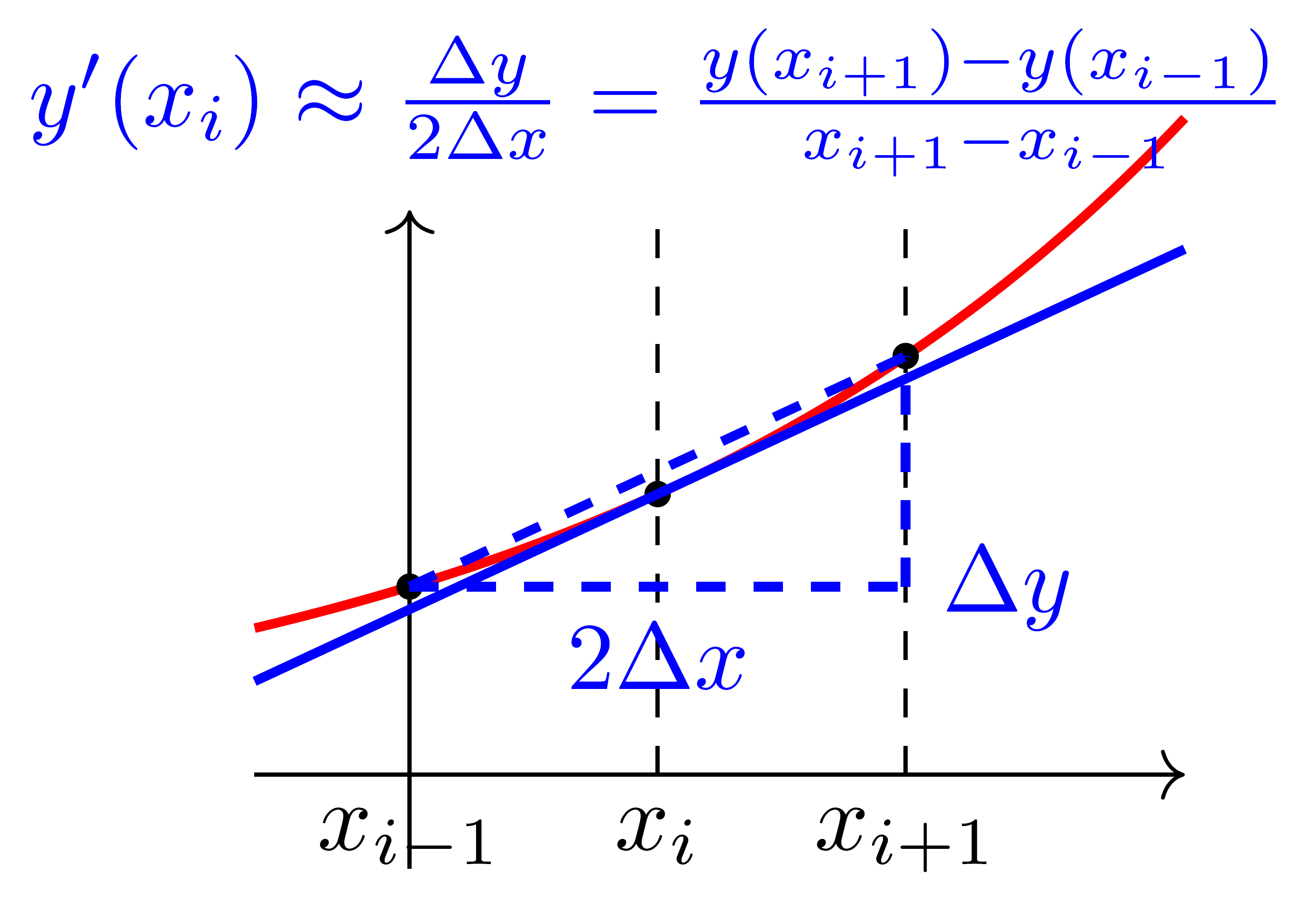
Rückwärtsdifferenzen, die Funktionswerte kleiner als x mit einbeziehen, zum Beispiel \(f'(x) \approx \frac{f(x) - f(x-dx)}{dx}\).
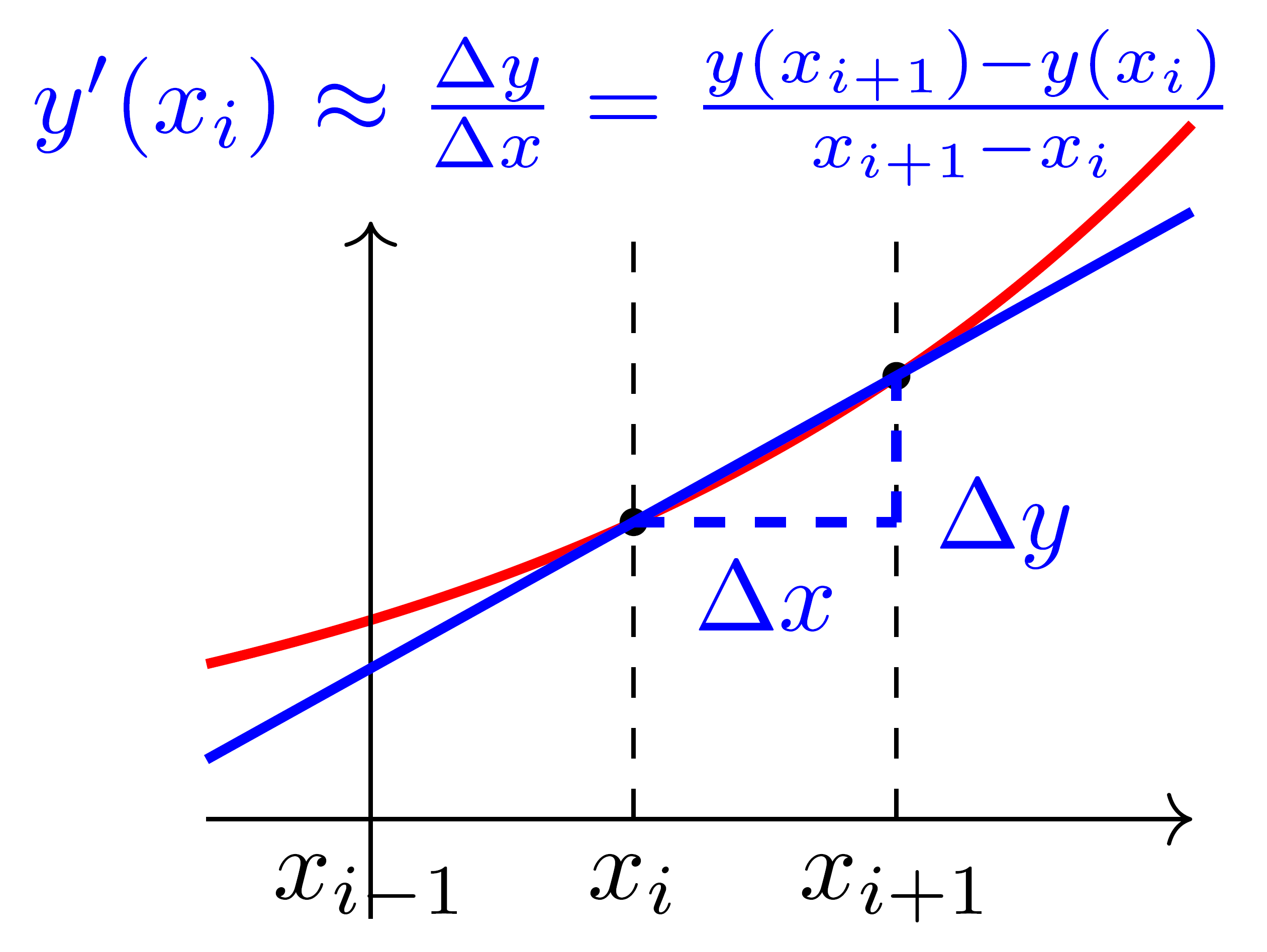
Differenzenquotienten können für beliebig hohe Ableitungen gebildet werden. Der Fehler wird mit geringerer Schrittweite \(dx\) kleiner. Wie stark der Fehler kleiner wird, beschreibt die Fehlerordnung \(\mathcal{O}\). Zum Beispiel ist für quadratische Fehlerordnung, bezeichnet durch \(\mathcal{O}(dx^2)\), bei halber Schrittweite der Fehler nur ein Viertel so groß, also \(dx_2 = \frac{dx_1}{2} \rightarrow \epsilon_2 = \frac{\epsilon_1}{2^2}\).
Hinweis
Anstelle von \(dx\) wird oft auch \(h\) als Symbol für die Schrittweite verwendet.
Aufgabe 1¶
Stellen Sie eine Übersicht und Bewertung verschiedener Differenzenquotienten für verschiedene Ableitungen auf. Schreiben Sie dazu ein Skript, das für eine Auswahl von Funktionen die numerische Approximation an einigen Stellen mit Ihrer analytischen Lösung vergleicht. Suchen Sie sich einige Beispiele für Differenzenquotienten aus den Lehrunterlagen oder von Wikipedia.
Beantworten Sie für einige Ableitungen erster und zweiter Ordnung die folgenden Fragen:
Welche Funktionstypen lassen sich mit bestimmten Differenzenquotienten besonders gut lösen? Welche besonders schlecht?
Wie teuer sind höhere Fehlerordnungen? Lohnen sich die zusätzlichen Funktionsauswertungen?
%%%your code here%%%
Aufgabe 2¶
Erstellen Sie nun für die Differenzenquotienten jeweils eine Test-Funktion.
Lagern Sie Ihren Test so aus, dass Sie für beliebige Funktionen die eingegebene analytische Lösung mit der numerischen Lösung vergleichen können.
Werten Sie anstatt für diskrete Werte, nun für ganze Intervalle die durchschnittliche und die maximale Abweichung
meandiff,maxdiffvon der analytischen Lösung aus.Werten Sie die benötigte Zeit
timeund die Anzahl an Funktionsauswertungennaus.Verringern Sie die Anzahl der Funktionsauswertungen, indem Sie diese wiederverwenden.
Hinweis
Bei sehr komplexen Funktionen ist die Verringerung von Funktionsauswertungen entscheidend für die Performanz Ihres Programms.
% f is function
% g is first derivative
% h is second derivative
% t is relevant interval
% dx is stepsize
function [meandiff, maxdiff, time, n] = test_<Name_Differenzenquotient>(f,g,h,t,dx)
tic;
time = toc;
end

 Github Repository
Github Repository