Modellierung einer Highline - Zeitliche Auflösung¶

Sie kennen dieses Modell einer Highline bereits aus dem Kapitel zu linearen Gleichungen. Alle wichtigen Informationen finden Sie in dem Kapitel Modellierung einer Highline, genauer Kräftebilanzierung.

Neu: Die dynamische Simulation¶

Anstatt einen stationären Lastfall zu betrachten und so die Gleichung zu \(S \tilde{\mathbf{z}} =\mathbf{b}\) zu vereinfachen, betrachten wir weiterhin die oben stehende Gleichung inklusive der Dämpfungsmatrix \(\mathbf{D}\). Die \(L = 50 \text{ m}\) lange Highline wird mit \(N = 100\) Elementen diskretisiert.

Nehmen Sie als Gesamtgewicht \(m_{ges} = 3.15 \text{ kg}\), als Dämpfung der Elemente \(d = 10 \,\frac{\text{Ns}}{\text{m}}\) und als Steifigkeit der Elemente \(k = 2\cdot10^4 \,\frac{\text{N}}{\text{m}}\) an.

Zur Erinnerung, das Gleichungssystem und die Matrizen sind:

\[M \ddot{\mathbf{z}} + D\dot{\mathbf{z}} + K \mathbf{z} = \mathbf{F}_{\text{ext}}, K = k \cdot S, D=d \cdot S, \]

\[\begin{split} \mathbf{z}=\left[ \begin{array}{c} \mathbf{z}_1 \\ \vdots \\ \mathbf{z}_N \end{array} \right] \in \mathbb{R}^{2N}, \quad \mathbf{F}_{\text{ext}} = \left[ \begin{array}{c} \mathbf{F}_{1,\text{ext}} \\ \vdots \\ \mathbf{F}_{N,\text{ext}} \end{array} \right] \in \mathbb{R}^{2N}, \quad M = \left[ \begin{array}{cccc} m & 0 & \cdots & 0 \\ 0 & m & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & m \end{array} \right] \in \mathbb{R}^{2N \times 2N} \quad \text{und} \end{split}\]

\[\begin{split}S = \left[ \begin{array}{rrrrrrr} 2 & 0 & -1 & 0 & \cdots & \cdots & 0 \\ 0 & 2 & 0 & -1 & \ddots & & \vdots \\ -1 & 0 & 2 & 0 & \ddots & \ddots & \vdots \\ 0 & -1 & 0 & 2 & \ddots & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & -1 \\ \vdots & & \ddots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & -1 & 0 & 2 \end{array} \right] \in \mathbb{R}^{2N \times 2N}.\end{split}\]

Aufgabe 1¶

Lösen Sie die Differentialgleichung mit der Matlab–Routine ode15s auf einem Zeitinterval von 40 Sekunden. Als externe Kraft \(\mathbf{F}_{ext}\) soll zunächst nur die Schwerkraft auf die Highline-Knoten wirken. Verwenden Sie \(\mathbf{z}(0)=\mathbf{\dot{z}}(0)=0\) als Anfangsbedingungen. Zunächst nehmen wir \(\mathbf{F}_{ext} = \text{const.} = \mathbf{F}_g\) an.

Tipp

Bringen Sie die DGL auf die Form

\[\begin{split}\mathbf{\dot{q}}=F(t,\mathbf{q})\text{, mit } \mathbf{q} = \left[ \begin{array}{c} \mathbf{q}_0 \\ \mathbf{q}_1 \end{array} \right] := \left[ \begin{array}{c} \mathbf{z} \\ \mathbf{\dot{z}} \end{array} \right] \in \mathbb{R}^{4N}\end{split}\]

mit einer geeigneten Funktion \(F:\mathbb{R}^{4N}\to\mathbb{R}^{4N}\)

Mit Ihrem Parameter L und den Ausgaben [t,q] aus ode15s können Sie die hinterlegte Funktion animate_highline(L,t,q) nutzen, um sich eine Animation Ihrer Simulation anzeigen zu lassen. Keine Sorge: In dieser Teilaufgabe darf die Auslenkung der Highline noch unrealistisch hoch sein.
Holen Sie sich Inspiration aus den vorherigen Aufgaben, insbesondere aus der Simulation eines Raketenstarts.
Sie müssen \(k\) anhand der Dehnbarkeit abhängig von der Länge Ihrer Elemente berechnen.

% space for the solution

% S = ...
% M = ...
% K = ...
% D = ...
% F = ...

% z = ...
% q = ...
% tspan = ...
% q0 = ...

%highlineode = ...

[t,q] = ode15s(highlineode,tspan,q0);

Hinweis

Die Animation kann nicht interaktiv auf dieser Seite laufen. Laden Sie sich die Dateien herunter und rechnen Sie lokal auf Ihrem Computer.

function animate_highline(L,t,q,person_on_highline)

dt = 0.2;                % time step size for animation
Ta = min(t);           % start time
Te = max(t);           % end time

N = floor(size(q,2)/4);  % get number of mass points from q
n = 2*N;

%% animating
timestep=0;
for ti=Ta:dt:Te
    timestep = timestep + 1;
    
    %get current displacement (interp1 is too slow)
    [~,i]=min(abs(t-ti));
    qi = q(i,:);
    
    %position of mass points = initial position + displacement
    positions_x = qi(1:2:n)+L*linspace(1/(N+1),1-1/(N+1),N);
    positions_y = qi(2:2:n);
    
    % x and y values of the highline nodes
    Xvalues=[0 positions_x L];
    Yvalues=[0 positions_y 0];
    
    if nargin>3
        % positions of the pedestrians
        posx = person_on_highline.positions(ti);
        posy = interp1(Xvalues,Yvalues,posx);
        if posx < L
            posxs(timestep) = posx;
            posys(timestep) = posy;
        else
            posxs(timestep) = L;
            posys(timestep) = 0;
        end
    end
    
    %% plot the animation of the highline with pedestrians
    cla;
    hold on
    plot(Xvalues,Yvalues,'-b', 'linewidth',1.5);
    if nargin>3
        scatter(posx,posy,50,'fill');
        plot(posxs,posys,'-r', 'linewidth', 1.5);
    end
    %axis equal
    box on
    ylim([-1.5,0.1]);
    xlim([0,L]);
    title(['t = ',num2str(ti,'%1.2f'),' s'])
    xlabel('horizontal direction [m]')
    ylabel('vertical direction [m]')
    
    drawnow
end

% plot the displacement of the slackline based on the solution vector z as well as the length of the slackline L
% (the function animate_highline is provided for you, you do not need to implement this)
animate_highline(L,t,q)

So sollte die sich einschwingende Highline aussehen:

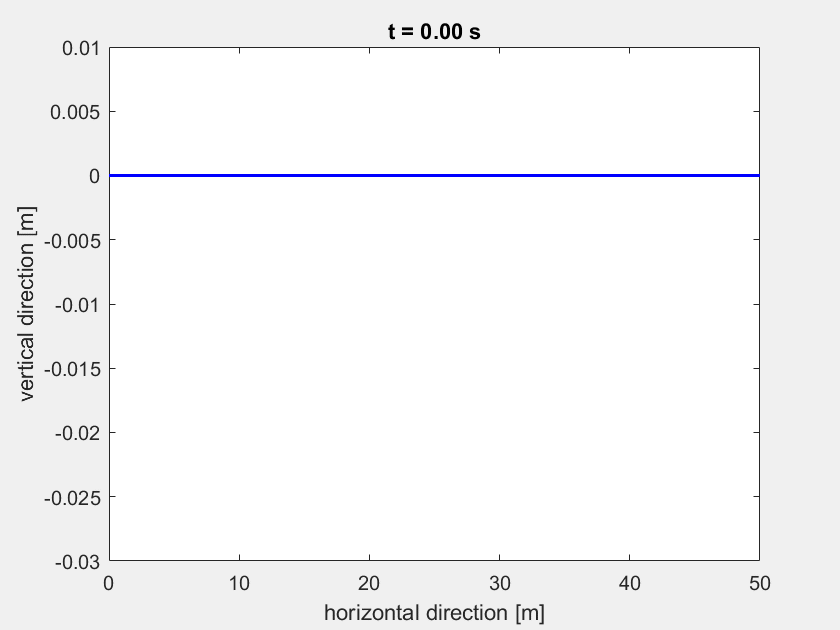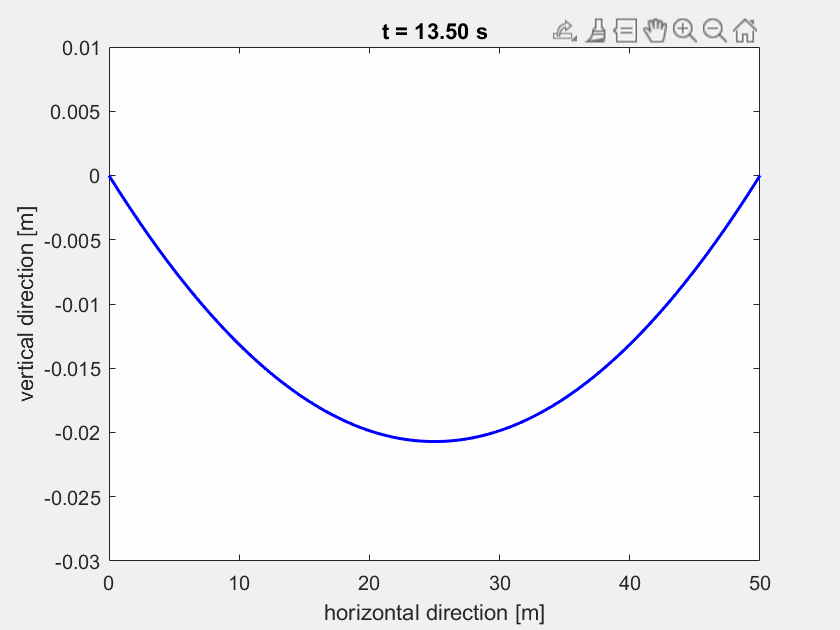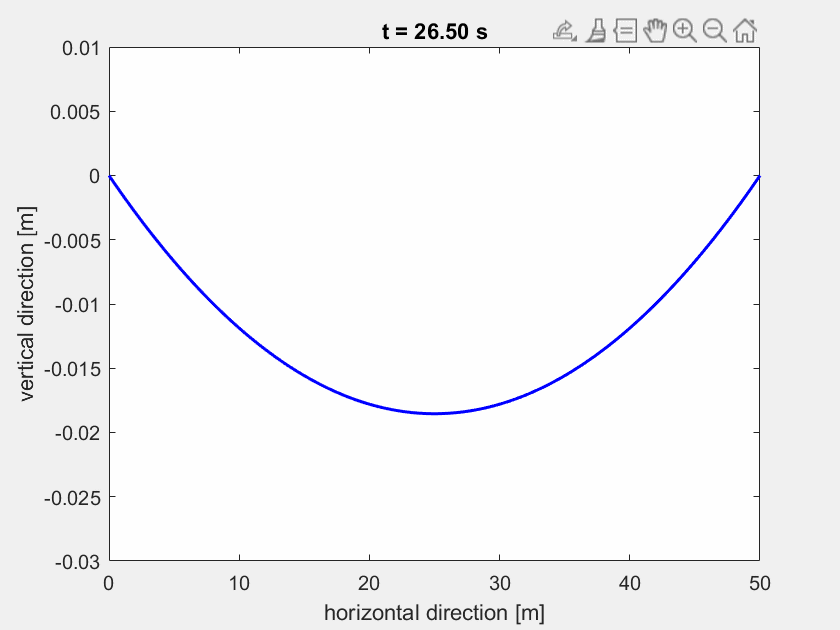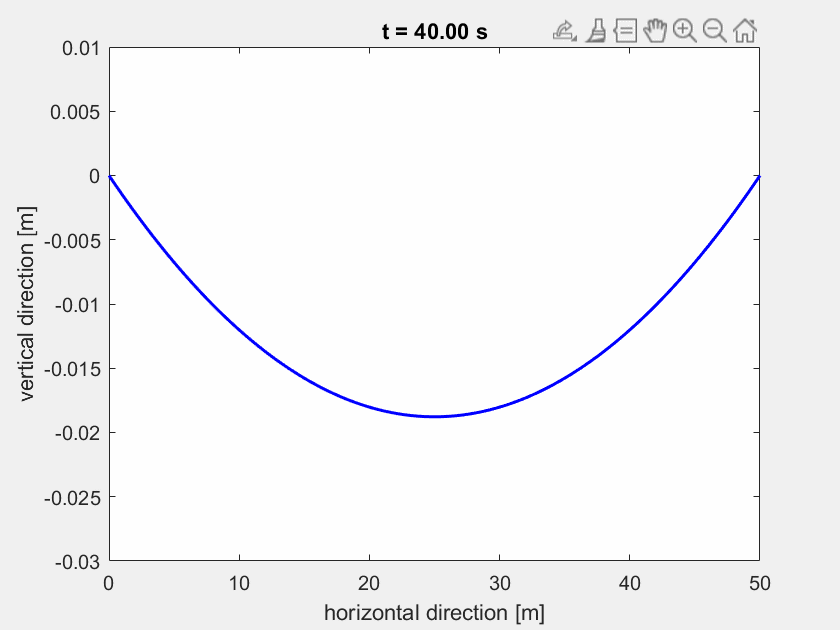
Aufgabe 2¶

Modifizieren Sie Ihr Skript so, dass zusätzlich zur Schwerkraft \(\mathbf{F}_g\) eine Anregung durch Wind \(\mathbf{F}_w\) sowie eine Anregung \(\mathbf{F}_p\) durch den Highliner modeliert wird, also

\[\mathbf{F}_{ext}(t) = \mathbf{F}_g + \mathbf{F}_w(t) + \mathbf{F}_p(t).\]

Simple Modelle für den Highliner und den Wind sind für Sie in wind.m und person_on_highline.m hinterlegt. Diese können Sie mit den Befehlen

classdef person_on_highline < handle
    % person_on_highline is an object to create the excitation caused by
    % a person on a highline.
    properties
        N;                  % no. of nodes of the highline (i.e. mass points)
        L;                  % length of the highline [m]
        weight = 75;        % weight of the person
        velocity = 0.4;     % velocity of the person [m/s]
    end
    methods
        %% constructor (creates the object)
        function p = person_on_highline(N,L)
            p.N = N;
            p.L = L;
        end % constructor
        
        %% excitation function
        function F = excitation(obj,t)
            
            % allocate output vector
            F=zeros(2*obj.N,1);
            
            %length of a highline segment between two nodes
            seglen = obj.L/(obj.N+1);
            
            %position of the person
            x=obj.velocity*t;
            
            %restrict position and weight to the highline
            weight=obj.weight(x<=obj.L);
            x=x(x<=obj.L);
            
            if ~isempty(x)
            %find the two nearest nodes to the person
                N0=floor(x/seglen);
                N1=ceil(x/seglen);

                %distribute the weight of the person to the two
                %nearest nodes
                a=(x-N0*seglen)/seglen;
                if N0>0 && N0<obj.N+1
                    F(2*N0)=-(1-a)*weight*9.81;
                end
                if N1>0 && N1<obj.N+1
                    F(2*N1)=-a*weight*9.81;
                end
            end
        end %excitation function
        
        %% positions(t) returns the horizontal position of the person
        function x = positions(obj,t) %animate_highline can also be used with pedestrians.m, so the plural is kept
            
            %position of the person
            x=obj.velocity*t;
            
            %restrict position to the highline
            x=x(x<obj.L);
        end %positions
    end% methods
end

classdef wind < handle
    % wind is an object to create the excitation caused by
    % wind on a highline.
    properties
        amplitude = 0.1;        % amplitude of the nodal forces due to wind [N]
        frequency = 5.39506;    % frequency of the nodal forces due to wind [1/s]
        weights;                % nodal weights for the force evaluation
    end
    methods
        %% constructor (creates the object)
        function w = wind(N)
            w.weights = (1-linspace(-1,1,2*N).^2)';
        end % constructor
        %% excitation function
        function F = excitation(obj,t)
            
            F=obj.amplitude*obj.weights*sin(obj.frequency*t);
            
        end %excitation function
    end% methods
end

storm = wind(N);
highliner = person_on_highline(N,L);

initialisieren. Achten Sie dazu auf die korrekte Belegung von N und L. Anschließend erhalten Sie \(\mathbf{F}_w(t)\) und \(\mathbf{F}_p(t)\) über die Ausdrücke

\(\mathbf{F}_w(t) = \)storm.excitation(t),

\(\mathbf{F}_p(t) = \)highliner.excitation(t).

Hinweis

Sollten Sie offline in Octave arbeiten, speichern Sie wind.m und person_on_highline.m in separaten Dateien.

Simulieren Sie die Highline für den Zeitraum, den die Person zur Überquerung benötigt. Erstellen Sie eine Animation mit dem Befehl animate_highline(...).

Animation nur mit Wind (mit animate_highline(L,t,q)):

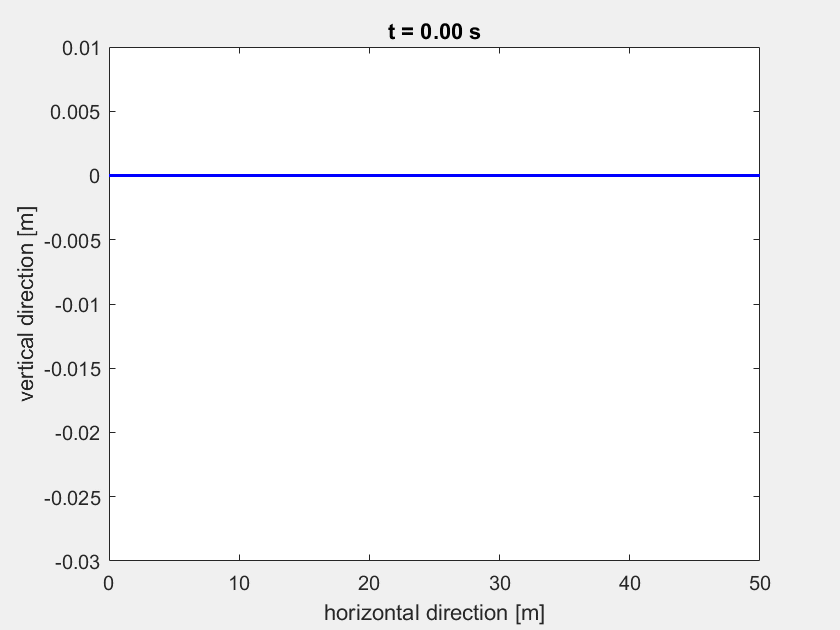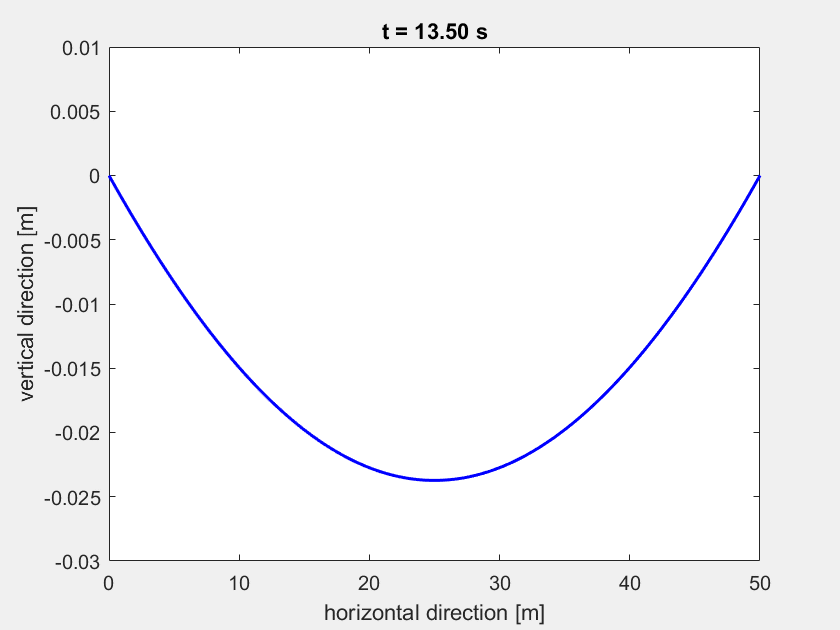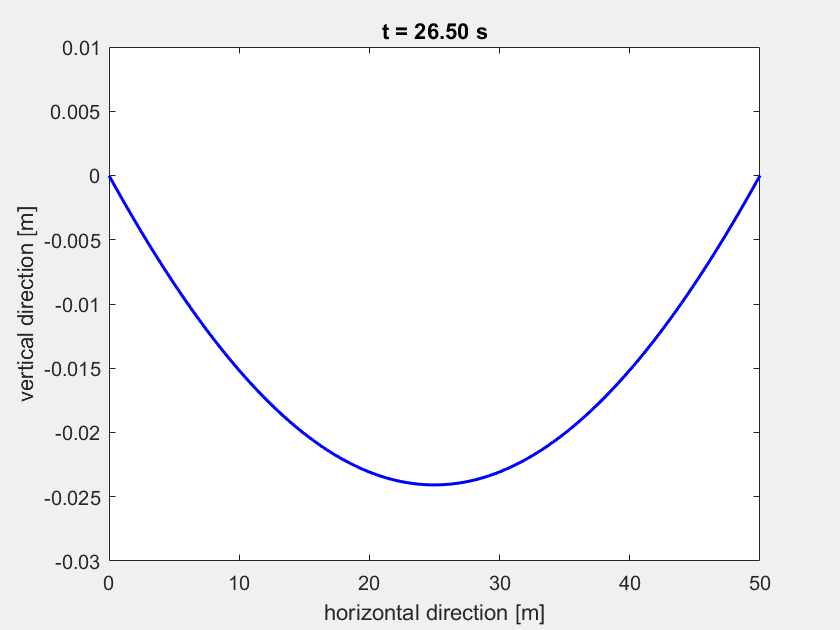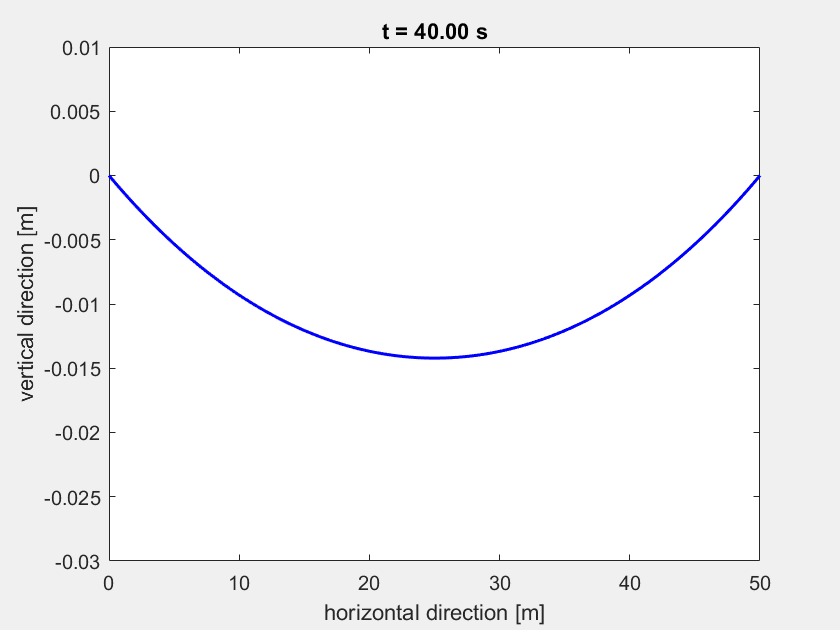
Animation mit Wind und Person auf der Highline (mit animate_highline(L,t,q,highliner)):

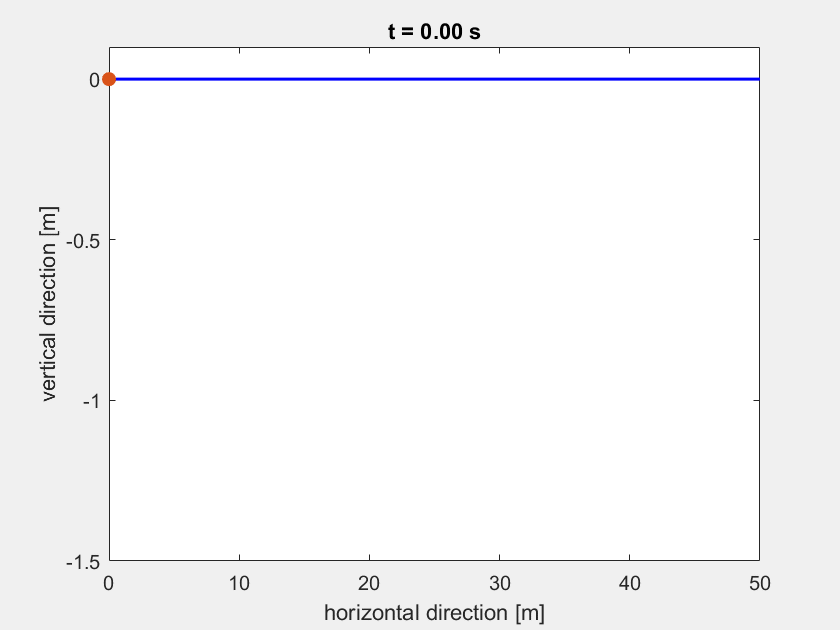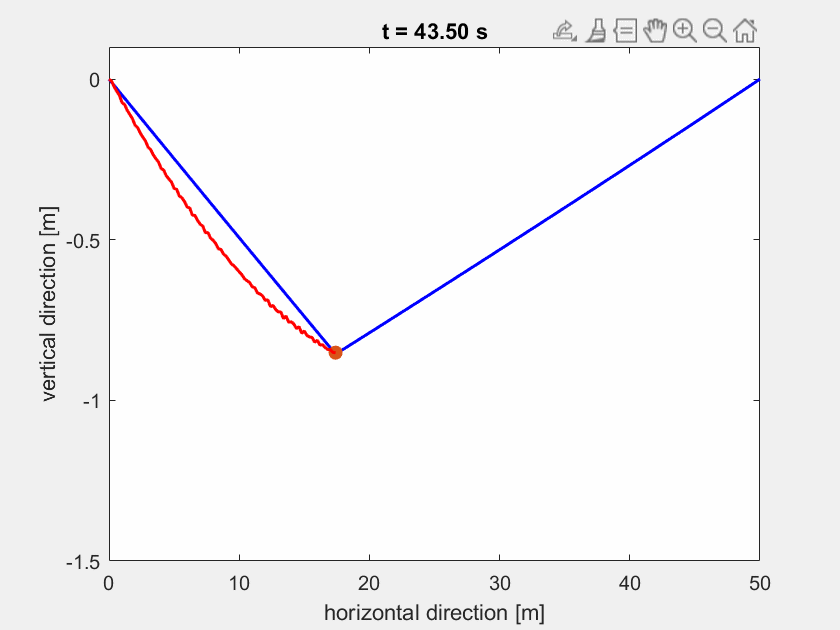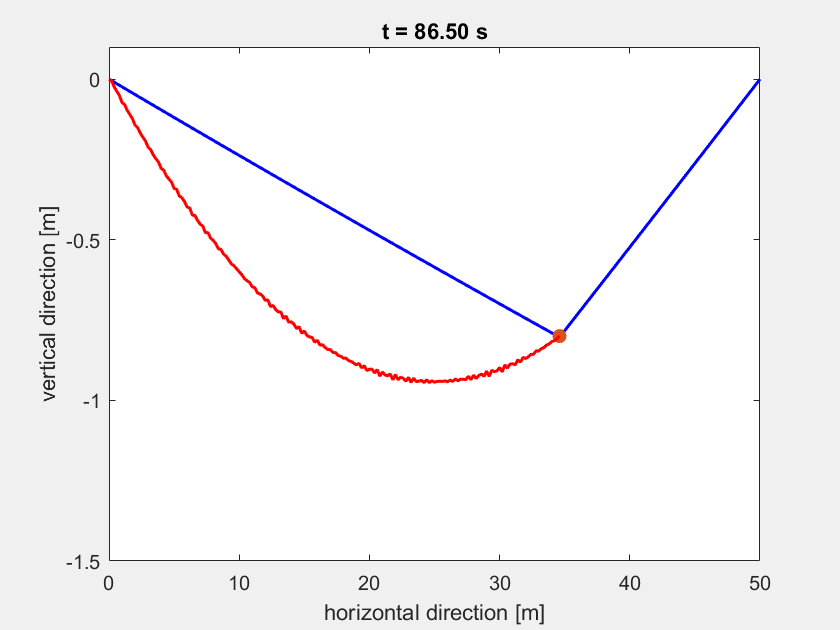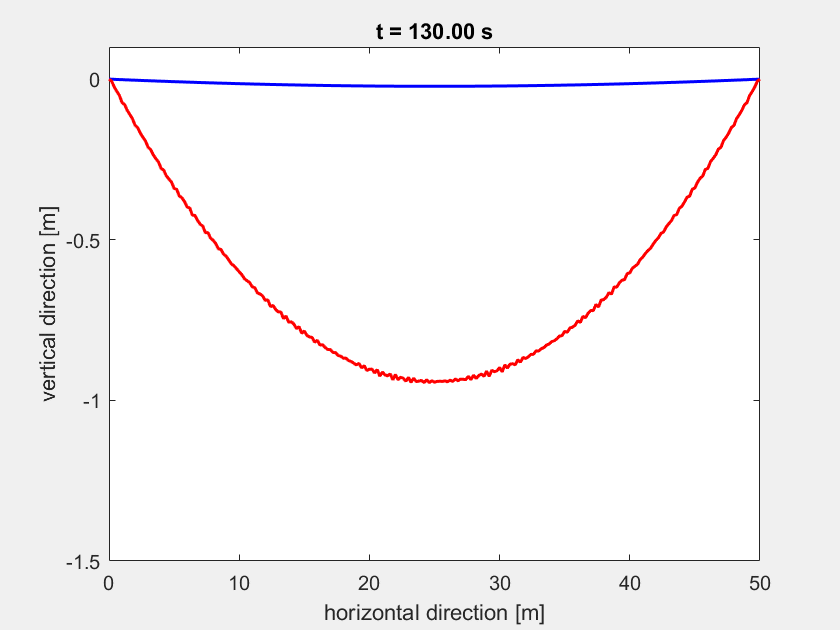
Aufgabe 3¶

Modifizieren Sie Ihr Skript, sodass es die folgenden Plots erstellt:

Ein Plot, der die Verschiebung der Mitte der Highline über die Zeit darstellt.
Ein Plot, der die Beschleunigungen der Mitte der Highline über die Zeit darstellt.

Gibt es eine einfache Maßnahme, mit der für die gegebene Anregung \(\mathbf{F}_{ext}\) die Schwingungsamplitude der Highline verringert werden kann? Belegen Sie Ihre Antwort möglichst mit Simulationsergebnissen. Wie gut lässt sich Ihre Maßnahme in der Praxis umsetzen?

Aufgabe 4¶

Reale Slacklines haben eine Dehnung von etwa \(15 \,\text{%}\) bei \(15 \,\text{kN}\) und ein Gewicht von etwa \(60 \,\frac{\text{g}}{\text{m}}\) (je nach Modell).

Wie können Sie die Dehnung in die Federsteifigkeit für variable \(L\) übertragen? Können Sie unabhängig von \(N\) die gleichen Ergebnisse erzielen?
Probieren Sie anstelle von ode15s den ‘klassischen’ Löser ode45 aus. Warum benötigt dieser so lang und warum ist ode15s so viel performanter? Lassen Sie sich dazu Eckdaten der Löser ausgeben.
Wirkt die Dämpfung realistisch? Lässt sich das System auch mit einer geringeren Dämpfung gut simulieren?

Modellbildung und Simulation

Modellierung einer Highline - Zeitliche Auflösung

Contents

Modellierung einer Highline - Zeitliche Auflösung¶

Neu: Die dynamische Simulation¶

Aufgabe 1¶

Aufgabe 2¶

Aufgabe 3¶

Aufgabe 4¶