10. Differential-Algebraische Gleichungen (2)¶

In dieser Übung wird das Schwingen eines Pendels simuliert. Dabei ist es möglich, die Bewegung als ODE- oder auch als DAE-System zu beschreiben. Wie unterscheiden sich das jeweils resultierende System und dessen Ergebnisse?

Situation¶

Die Bewegung eines Pendels kann sowohl als gewöhnliche Differentialgleichung (ODE) sowie auch als Differential-Algebraisches System (DAE) beschrieben werden.

1. Programmimplementierung¶

Lösen Sie die Pendelbewegung mithilfe von ein_pendel_dae.m.

%% file ein_pendel_dae.m
% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
global g m
g = 9.81; l = 0.15; m = 0.05;
y0 = [l 0 0 0 1]; tspan = [0, 3];
M = eye(5); M(5,5) = 0;
options = odeset('Mass',M,'RelTol',1.0e-5,'Stats','on');
tic
[t,y] = rodasp2(@dgl, tspan, y0,options);
toc
axis equal; hold on;
lges=1.2*l; r1 = 0.005; d1=2*r1;
axis ([-lges lges -lges 0.1*lges])
linie1 = line([0 y0(1)],[0 y0(3)]);
kugel1 = rectangle ('Position',[y0(1)-r1 y0(3)-r1 d1 d1],...
'Curvature', [1 1], 'Facecolor', 'r');
for i = 1:length(t)
    set(kugel1, 'Position', [-r1+y(i,1) -r1+y(i,3) d1 d1]);
    set(linie1, 'Xdata', [0 y(i,1)], 'Ydata', [0 y(i,3)]);
    drawnow
    if(i<length(t)) pause ((t(i+1)-t(i)));
    end
end

function dz = dgl(t,z)
    global g m
    dz(1,1) = z(2);
    dz(2,1) = 2*z(5)*z(1)/m;
    dz(3,1) = z(4);
    dz(4,1) = -g + 2*z(5)*z(3)/m;
    % dz(5,1) = z(1)^2 + z(3)^2-l^2; %Index = 3
    % dz(5,1) = z(1)*z(2) + z(3)*z(4); %Index = 2
    dz(5,1) = 2*(z(2)^2+z(1)*dz(2,1)+z(4)^2+z(3)*dz(4,1)); %Index
end

Die Funktion rodasp2 finden Sie hier.

2. Pendellänge¶

Leiten Sie aus den Simulationsergebnissen die Pendellänge her und überprüfen Sie, ob sie sich mit der Zeit verändert.

Plotten Sie die eventuelle Längenänderung über die Simulationszeit.

% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
% your code here

3. Systemdämpfung¶

Bringen Sie eine Dämpfung in das System ein.

4. Pendel als ODE¶

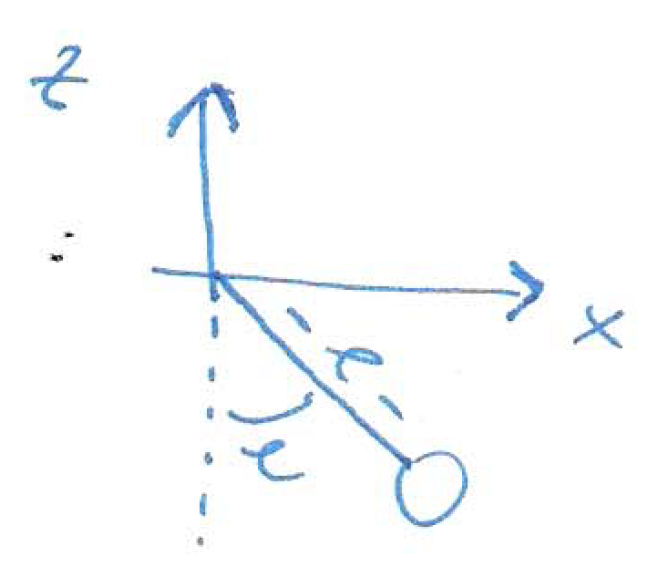
Das Pendel kann auch als ODE beschrieben werden (Drehbewegung). Der Drehwinkel definiert sich dann wie folgt:

\[\ddot{\varphi}=-\frac{g}{L}\sin(\varphi)\]

Dabei ist der Winkel so festgelegt, dass \(\varphi(t)=0\) für ein senkrecht nach unten zeigendes Pendel gilt. Implementieren Sie diese Gleichung und vergleichen Sie die Lösungen der beiden Ansätze.

% your code here

Lösung¶

- Hinweis: Dieses Video ist von YouTube aus eingebunden und nicht Teil des frei lizenzierten Materials! -

Zusatzaufgabe: Doppelpendel¶

Leiten Sie die Gleichungen eines Doppelpendels her und implementieren Sie diese.

Modellbildung und Simulation

10. Differential-Algebraische Gleichungen (2)

Contents