Contents

Systeme von ODEs

Voraussetzungen

  • Runge-Kutta-Verfahren zur numerischen Integration von gewöhnlichen Differentialgleichungen

Lerninhalte

  • Lösen von mehrdimensionalen gewöhnlichen Differentialgleichungen

Systeme von ODEs

Aufgabe 1: Schwingung eines Pendels

Die Schwingungsgleichung eines Pendels lernen Sie auch in dem Kapitel Harmonische Schwingung kennen. Da lösen Sie sie mit ode45.

Nun gehen Sie einen Schritt weiter:

  • Stellen Sie die Schwingungsgleichung für sowohl mit als auch ohne Kleinwinkelnäherung auf.

  • Formen Sie die resultierende ODE zweiter Ordnung in ein System von zwei ODEs um.

  • Implementieren Sie nun eines Ihrer Verfahren aus den Kapitel Integration von ODEs mit expliziten Verfahren und Integration von ODEs mit impliziten Verfahren zum Lösen der von Ihnen hergeleiteten Differentialgleichungen. Dazu muss Ihr Code auch mit Systemen von ODEs umgehen können.

Zur Erinnerung das Fadenpendel

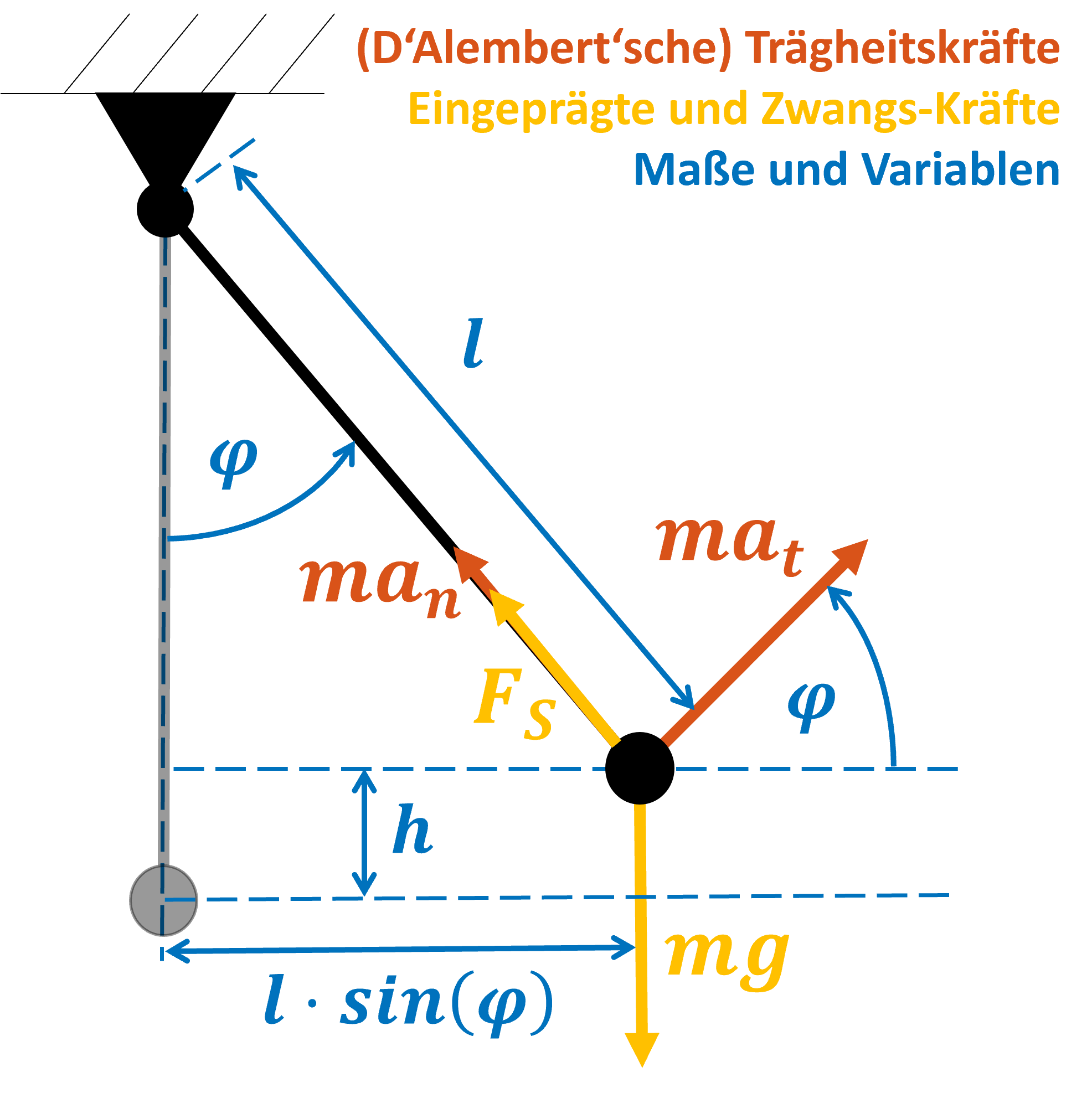
Name of image

Abbildung 1: Das Pendel als klassisches Schwingungsbeispiel. Eingezeichnet sind die Trägheitskräfte (rot), eingeprägte und Zwangskräfte (gelb) und Maße und Variablen (blau). Das Pendel ist im ausgelenkten (schwarz) und hängenden (grau) Zustand dargestellt.

%your code here

Aufgabe 2: Die van-der-Pol Gleichung

Die van-der-Pol Gleichung lautet

\[\ddot{x} - \varepsilon(1-x^2)\dot{x} + x = 0.\]

Analog zu dem Fadenpendel kann \(x\) als ein Winkel beziehungsweise eine Auslenkung interpretiert werden. Die van-der-Pol Gleichung stellt ein besonderes Problem für numerische Verfahren dar. Testen Sie anhand dieser Gleichung Ihre Lösungsverfahren und plotten Sie Ihr Ergebnis. Nehmen Sie auch die Dauern Ihrer Verfahren auf. Ihre Lösung könnte beispielsweise so aussehen:

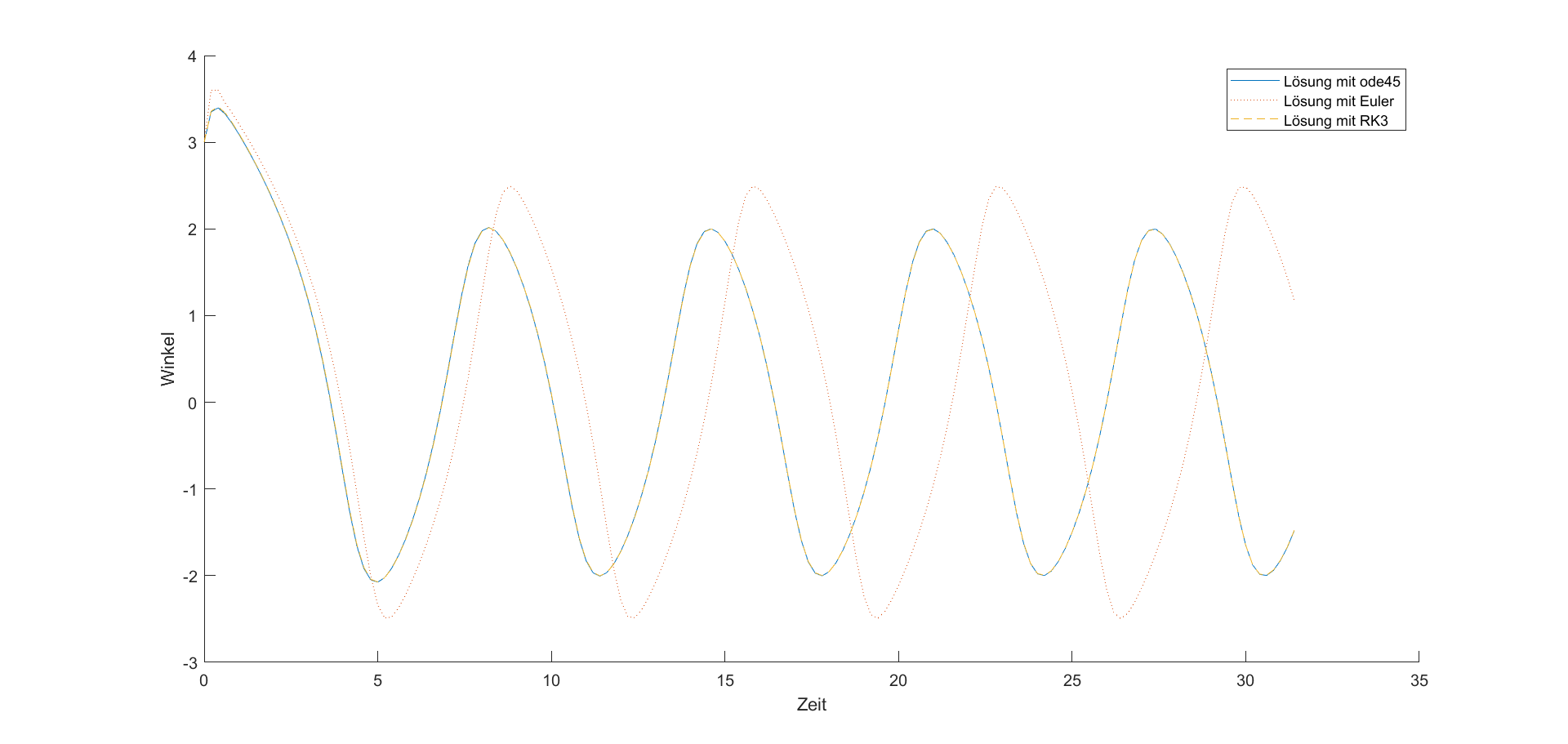
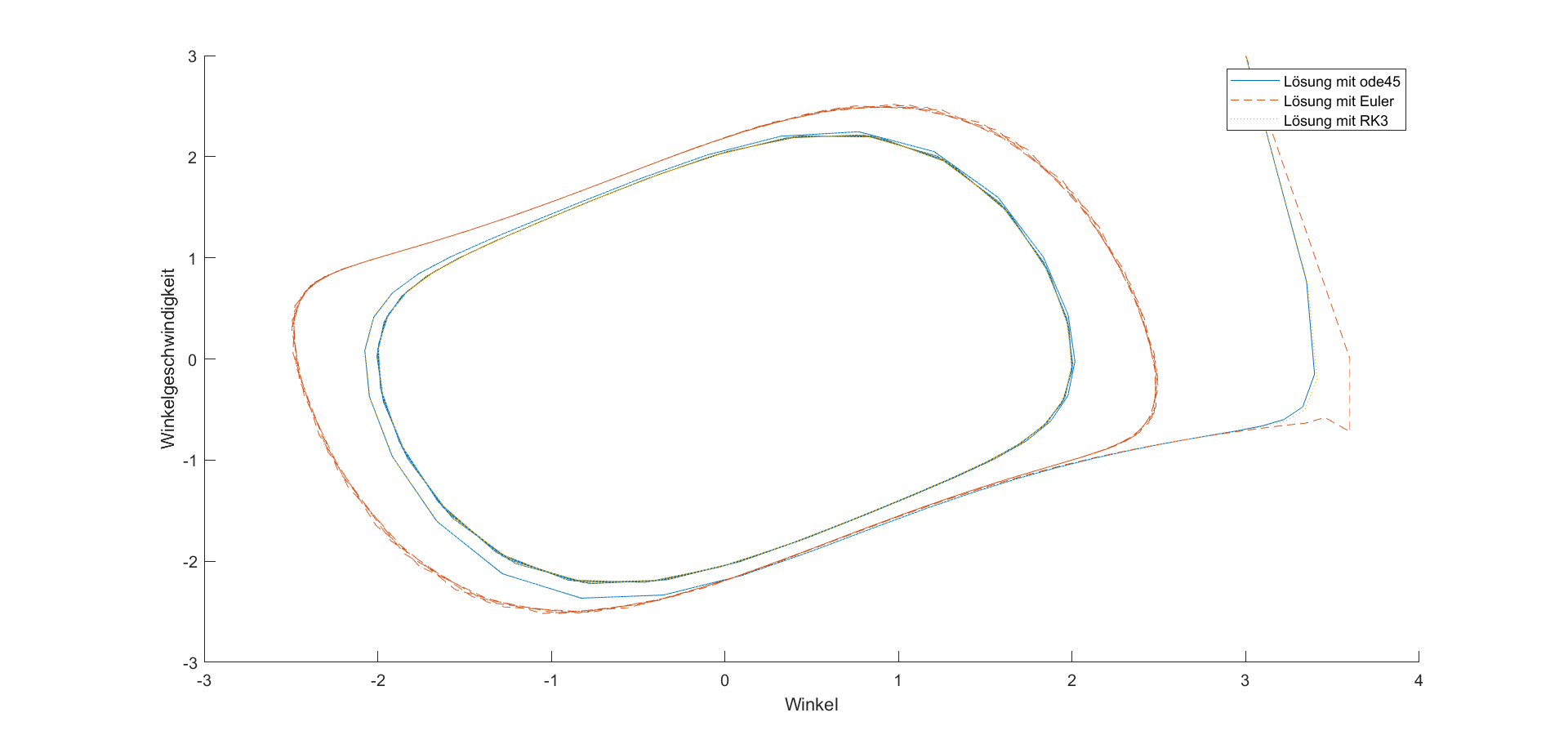
Name of image Name of image

Abbildung 2: Schwingung und Phasenraum verschiedener Lösungen der van-der-Pol Gleichung. Das explizite Eulerverfahren (rote Punkte) zeigt eine deutliche höhere Amplitude und verschobene Periode. Die Lösung mit einem Runge-Kutta-Verfahren dritter Ordnung (gelbe Striche) liegt sehr nah bei der sehr genauen Lösung von ode45 (blaue Linie).

%your code here

Aufgabe 3: Die inhomogene van-der-Pol Gleichung

Ein schwingfähiges System kann periodisch angeregt werden. Das ist besonders interessant für Resonanzfälle, die gewünscht oder unerwünscht sein können. Für eine periodisch angeregte van-der-Pol Schwingung lautet die Gleichung

\[\ddot{x} - \varepsilon(1-x^2)\dot{x} + x = A \cos(\omega t + \varphi_0).\]

previous

Adaptive Schrittweitensteuerung

next

Lohnen sich Verfahren höherer Ordnung?