9. Differential-Algebraische Gleichungen (1)¶

In dieser Übung wird das Rollen einer Kugel auf einer Bahn simuliert. Da die Bewegung der Kugel durch die Bahn eingeschränkt ist, handelt es sich um ein sog. DAE-System (Differential-Algebraic Equation).

Situation¶

Eine Kugel rollt eine Bahn hinab. Diese Bahn ist beschrieben durch

\[f(x) = \cos\left(\frac{x}{2}\right)+1\]

Die Kugel kann als DAE-System modelliert und anschließend ihr Rollen auf der Bahn simuliert werden.

1. Kugelbahn¶

Stellen Sie für die Bahn der Kugel eine eigene function auf und plotten Sie diese.

% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
%your code here

Ihr Ergebnis sollte so aussehen:

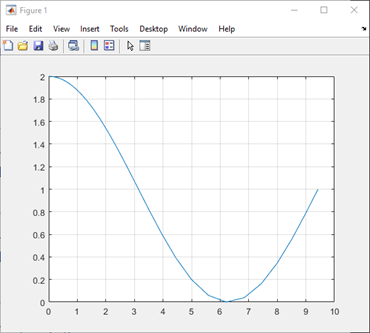
2. Modellbildung¶

Stellen Sie die Bewegungsgleichungen der Kugel auf. Formulieren Sie dazu die Zwangsbedingung (=Bahn) als Nullstellenproblem.

\[f(x,y)=0\]

Die Bewegungsgleichungen der Kugel ergeben sich aus der Kräftebilanz

\[\begin{split}m \left( \begin{array}{c} \ddot{x}\\ \ddot{y}\\ \end{array} \right) = \vec{F_\text{G}} + \vec{F_\text{R}}\end{split}\]

wobei sich die Zwangskraft \(F_\text{R}\) wie folgt berechnet:

\[\vec{F_\text{R}}=\lambda\cdot\text{grad}(f)\]

\[\begin{split}\text{grad}(f)=\left( \begin{array}{c} \ddot{\frac{\partial f}{\partial{x}}}\\ \ddot{\frac{\partial f}{\partial{y}}}\\ \end{array} \right)\end{split}\]

Nun haben Sie zwei Differentialgleichungen für die \(x\)-\(y\)-Bewegungen. Die Zwangsbedingung \(f(x,y)\) muss nun noch auf Index-1 reduziert werden.

Dazu wird \(f\) zweimal nach der Zeit abgeleitet. Beachten Sie, dass sowohl \(x\) als auch \(y\) zeitabhängige Variablen sind.

Abschließend muss das entstandene System (=3 Gleichungen) auf Ordnung 1 reduziert werden (= 5 Gleichungen), bevor es in Matlab implementiert werden kann. Das zu implementierende System sollte dann folgende Form haben:

\[q_1 = x, q_2 = \dot{x}, q_3 = y, q_4 = \dot{y}, q_5 = \lambda\]

\(\dot{q_1}=q_2\)
\(\dot{q_2}=\dots\)
\(\dot{q_3}=q_3\)
\(\dot{q_4}=\dots\)
\(\dot{q_5}=\frac{d^2}{dt^2}f(x,y)\)

3. Implementierung¶

Legen Sie zur Implementierung eine Programmstruktur ähnlich dem Lösen von ODEs an.

function main
    q0 = [0;0.1;2;0;0];
    tspan = [0,15];
    [t,q] = ode15s(@dae,tspan,q0);
end

function dq = dae(t,q)
    % Hier die Systemgleichungen einfügen
end

Zur Lösung benötigt der Solver Kenntnis über die Masse-Matrix des Systems. Diese definiert sich in diesem Fall als Einheitsmatrix, deren letzter Eintrag eine Null ist.

\[\begin{split}M = \begin{pmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{pmatrix}\end{split}\]

Definieren Sie daher vor dem Solver-Aufruf die Matrix \(M\) und übergeben Sie diese per folgender Codezeile:

options = odeset('Mass',M);

4. Simulation und Auswertung¶

Lassen Sie sich die Simulationsergebnisse als X-Y-Plot ausgeben.
Plotten Sie die vorgegebene Bahnkurve sowie die Ergebnisse der DAE-Berechnung übereinander. Folgt die Kugel auch der Bahn oder gibt es Abweichungen?
Definieren Sie folgende Events:
Detektion von y == 1, y == 0 und Stopp der Simulation, wenn die Kugel das zweite Mal y == 0 (ca. bei x == 9.4) erreicht.
Zu welchem Zeitpunkt \(t\) werden diese Werte jeweils erreicht?

% your code here

5. Zusatz: Dämpfung und animierter Plot¶

Ergänzen Sie zur Kräftebilanz eine verallgemeinerte Dämpfungskraft \(F_\text{d}=d\cdot\begin{pmatrix}\dot{x}\\\dot{y}\end{pmatrix}\), mit \(d=0.5\), sodass die Kugel nach einer gewissen Zeit zum Stillstand kommt.

Animieren Sie anschließend den Lauf der Kugel, indem Sie mittels for-Schleife die Ergebnisse pro Zeitschritt nacheinander anzeigen lassen.

% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
for i = 1:length(t)
    plot(q(i,1),q(i,3),'x')
    grid on
    axis([0,10,0,2])
    pause(0.05)
    drawnow
end

Lösung¶

- Hinweis: Dieses Video ist von YouTube aus eingebunden und nicht Teil des frei lizenzierten Materials! -

Modellbildung und Simulation

9. Differential-Algebraische Gleichungen (1)

Contents