Contents

Lohnen sich Verfahren höherer Ordnung?

Voraussetzungen

  • Schwingungen

  • Explizite und implizite Integrationsverfahren von gewöhnlichen Differentialgleichungen

  • gute Kenntnisse über die Implementierung der Lösungsverfahren

Lerninhalte

  • Bewertung einiger grundlegender Integrationmethoden

Lohnen sich Verfahren höherer Ordnung?

In diesem Kapitel stellen Sie Ihre erworbenen Grundkenntnisse über ODEs unter Beweis, stellen fest, ob sich Verfahren höherer Ordnung lohnen und beurteilen, welches Verfahren Sie in der Praxis verwenden würden.

Nachdem wir uns in den Kapiteln Integration von ODEs mit expliziten Verfahren und Integration von ODEs mit impliziten Verfahren auf das numerische Lösen einer analytisch nicht lösbaren ODE fokussiert haben, möchten wir nun bewerten, wie gut die numerische Lösung im Vergleich zur analytischen Lösung ist. Dazu nehmen wir das Beispiel des Fadenpendels aus dem Kapitel Harmonische Schwingung. Dessen Lösung kennen wir unter der Annahme der Kleinwinkelnäherung \(\sin \varphi \approx \varphi\):

\[\varphi(t) = \varphi_0 \cdot \cos \left( {\sqrt{\frac{g}{l}} \cdot t} \right)\]
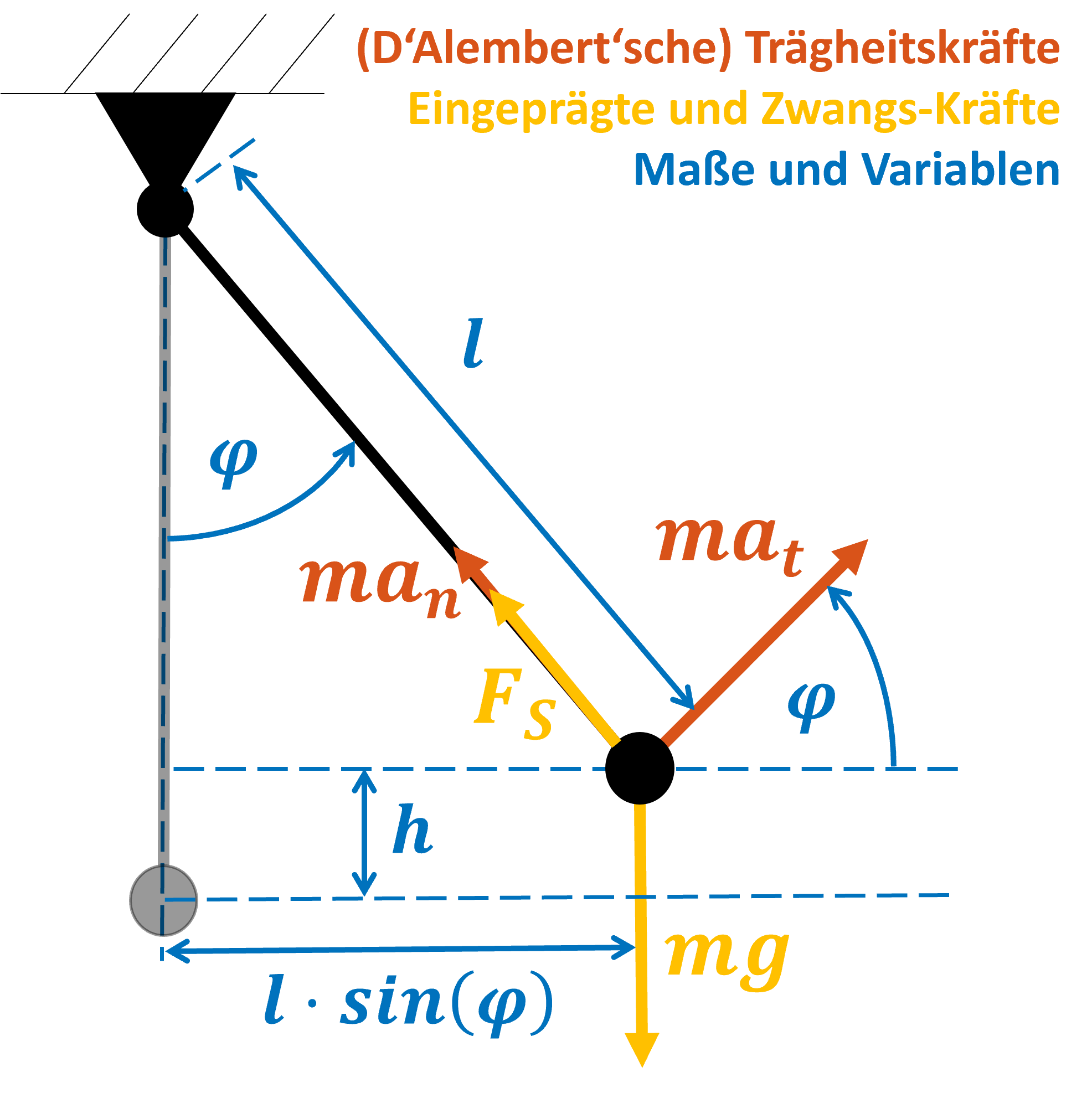
Name of image

Abbildung 1: Das Pendel als klassisches Schwingungsbeispiel. Eingezeichnet sind die Trägheitskräfte (rot), eingeprägte und Zwangskräfte (gelb) und Maße und Variablen (blau). Das Pendel ist im ausgelenkten (schwarz) und hängenden (grau) Zustand dargestellt.

Aufgabe 1: Analytische Lösung

Stellen Sie die analytische Lösung auf und plotten Sie sie mit einer hohen Auflösung (> 1000 Punkte). Gehen Sie von \(\varphi_0 = 1\) und \(\omega_0 = 1\) aus. Nehmen Sie auf Ihrem Intervall mindestens drei Perioden auf.

%your code here
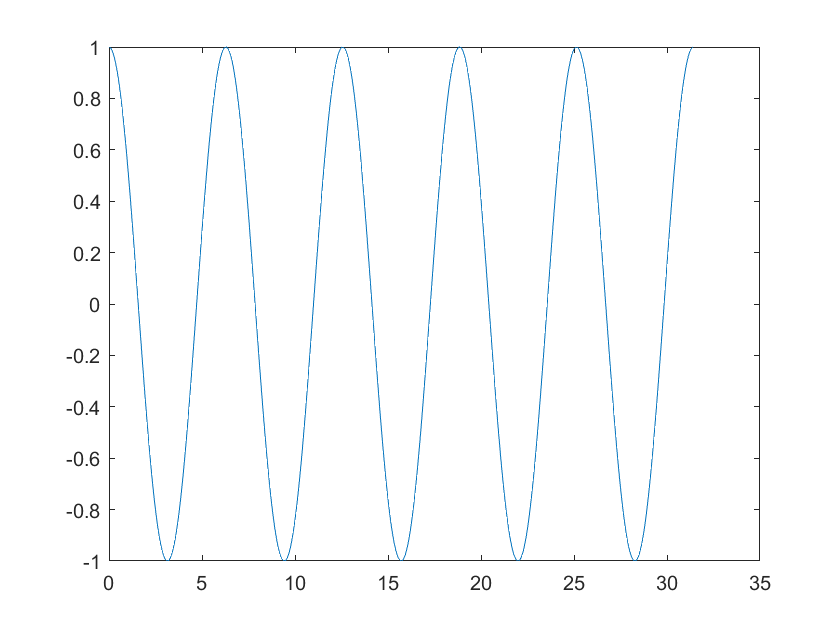
Name of image

Abbildung 2: Lösung des Fadenpendels als Kosinus-Funktion.

Aufgabe 2: Vergleich der verschiedenen Lösungen

Wir wollen hier folgende Lösungsmöglichkeiten vergleichen:

  1. explizites Eulerverfahren (Linke Rechteckregel)

  2. Runge-Kutta-Verfahren 2. Ordnung (Mittelpunktsregel mit Schätzung von \(y_{i+\frac{1}{2}}\)

  3. Runge-Kutta-Verfahren 3. Ordnung (Simpsonregel)

  4. implizites Eulerverfahren (Rechte Rechteckregel)

  5. implizite Trapezregel

Gehen Sie zunächst davon aus, dass alle Verfahren dieselbe Schrittweite (100 Punkte auf Ihrem Intervall) nutzen und verwenden Sie keine Schrittweitensteuerung.

%your code here
expEul   = ...
RK2      = ...
...

%plots
plot(tspan,expEul,tspan,RK2,...)

Ihre Lösung könnte in etwa so aussehen (hier mit einer Schrittweite von 0.1):

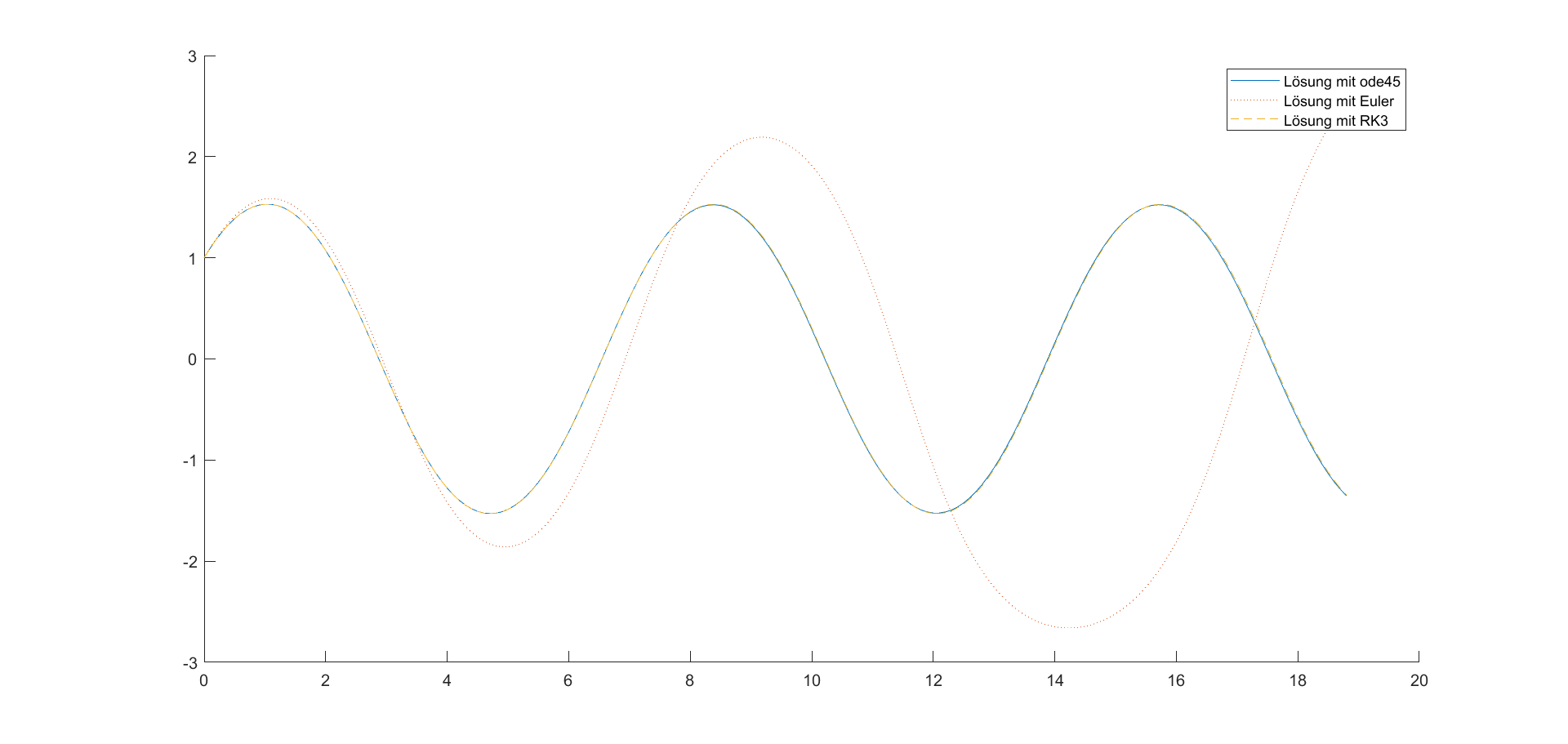
Name of image

Abbildung 3: Lösung des Fadenpendels als mit verschiedenen ODE-Lösern. Das explizite Eulerverfahren (rote Punkte) zeigt eine sich erhöhende Amplitude (siehe Hinweis). Die Lösung mit einem Runge-Kutta-Verfahren dritter Ordnung (gelbe Striche) liegt sehr nah bei der sehr genauen Lösung von ode45 (blaue Linie).

Achtung

Die Abweichung der Lösung können wir nun auch interpretieren! Wird die Amplitude der Schwingung größer, bedeutet das, dass dem System Energie zugeführt wurde. Und wir als Ingenieur:innen wissen: Das kann nicht sein. In der Praxis kann es sein, dass solche Abweichungen nicht so offensichtlich falsch sind. Es ist also immens wichtig, dass unsere Lösung an die reale Lösung gut konvergiert.

Messen Sie nun zusätzlich die benötigte Zeit der Verfahren mit den tic ... time_n = toc Befehlen sowie die Abweichung von der analytischen Lösung über den gesamten Zeitraum. Als Grundlage für eine quantitative Bewertung der Abweichung hat sich die Methode der Summe der Quadrate bewährt.

% time results
time_expEul = ...
time_RK2    = ...
...

% error results
err_expEul  = sum((...).^2);
err_RK2     = ...
...

Aufgabe 3: Vergleich anhand eines Goldstandards

Manchmal kennen wir bei einer Analyse von Problemen keine exakte Lösung. In solchen Fällen vergleichen wir für reduzierte Probleme besonders genaue (aber aufwendige!) Verfahren mit den von uns erstellten einfacheren Verfahren.

Vergleichen Sie die Verfahren aus Aufgabe 2 anhand der Traktrix.

\[f(x,y) = - \frac{y(x)}{\sqrt{d^2-y^2(x)}}\]

Nutzen Sie dazu als Goldstandard die Matlab-Routine ode45 und vergleichen Sie, auf welche Werte die Verfahren nach einer bestimmten Strecke \(x_\text{end}\) kommen.

function ydot = dgl(y,d)
    ydot = -y/sqrt(d^2-y^2);
end

% calculations
...

% time results
time_expEul = ...
time_RK2    = ...
...
time_ode45  = ...

% error results
err_expEul  = abs(y_expEul(end) - y_ode45(end));
err_RK2     = ...
...

Aufgabe 4: Lohnt sich das?

Um zu ermitteln, wie lang die Verfahren benötigen, passen Sie die Schrittweiten der Verfahren so an, dass die relative Abweichung von der analytischen Lösung geringer ist als ein von Ihnen festgelegter Wert. Messen Sie die Zeit, die die Verfahren dafür benötigen, mit den tic toc Befehlen.

Hinweis

Diese Aufgabe können Sie auch mit einer adaptiven Schrittweitensteuerung aus dem Kapitel Adaptive Schrittweitensteuerung lösen.

  • Wie lang benötigen die Verfahren?

  • Für welches Verfahren entscheiden Sie sich in der Praxis?

%your code here

rtol = 1e-14;
tic
while err_expEul > rtol
    ...
end
time_expEul = toc

previous

Systeme von ODEs

next

Harmonische Schwingung