Integration von ODEs mit impliziten Verfahren¶

Wir wollen in diesem Kapitel wieder die Traktrix

\[f(x,y(x)) = y'(x) = - \frac{y}{\sqrt{d^2-y^2(x)}}\]

lösen, diesmal mit impliziten Verfahren.

Aufgabe 1: Die rechte Rechteckregel¶

Die rechte Rechteckregel lautet

\[\int_{x_i}^{x_{i+1}}f(x,y(x))dx \approx h \cdot f(x_{i+1},y_{i+1}).\]

Daraus leiten wir für die ODE

\[y_{i+1} \approx y_i + h \cdot f(x_{i+1},y_{i+1})\]

ab. Diese Gleichung können wir nach \(0\) umstellen, wodurch wir anstelle der ODE ein Nullstellenproblem für jeden Schritt lösen müssen.

\[0 = - y_{i+1} + y_i + h \cdot f(x_{i+1},y_{i+1}) := g(y_{i+1})\]

Die Nullstelle der Funktion \(g(y_{i+1})\) ist also unser gesuchter nächster Schritt.

Hinweis

Dieses Vorgehen entspricht dem impliziten Eulerverfahren, das in dem Kapitel Stabilität des expliziten versus impliziten Eulerverfahrens weiter dikutiert wird.

Vergleich mit der numerischen Integration skalarer Funktionen

Auch die impliziten Verfahren lassen sich mit der Integration algebraischer Funktionen vergleichen. Für die Integration einer bekannten Funktion \(f(x)\):

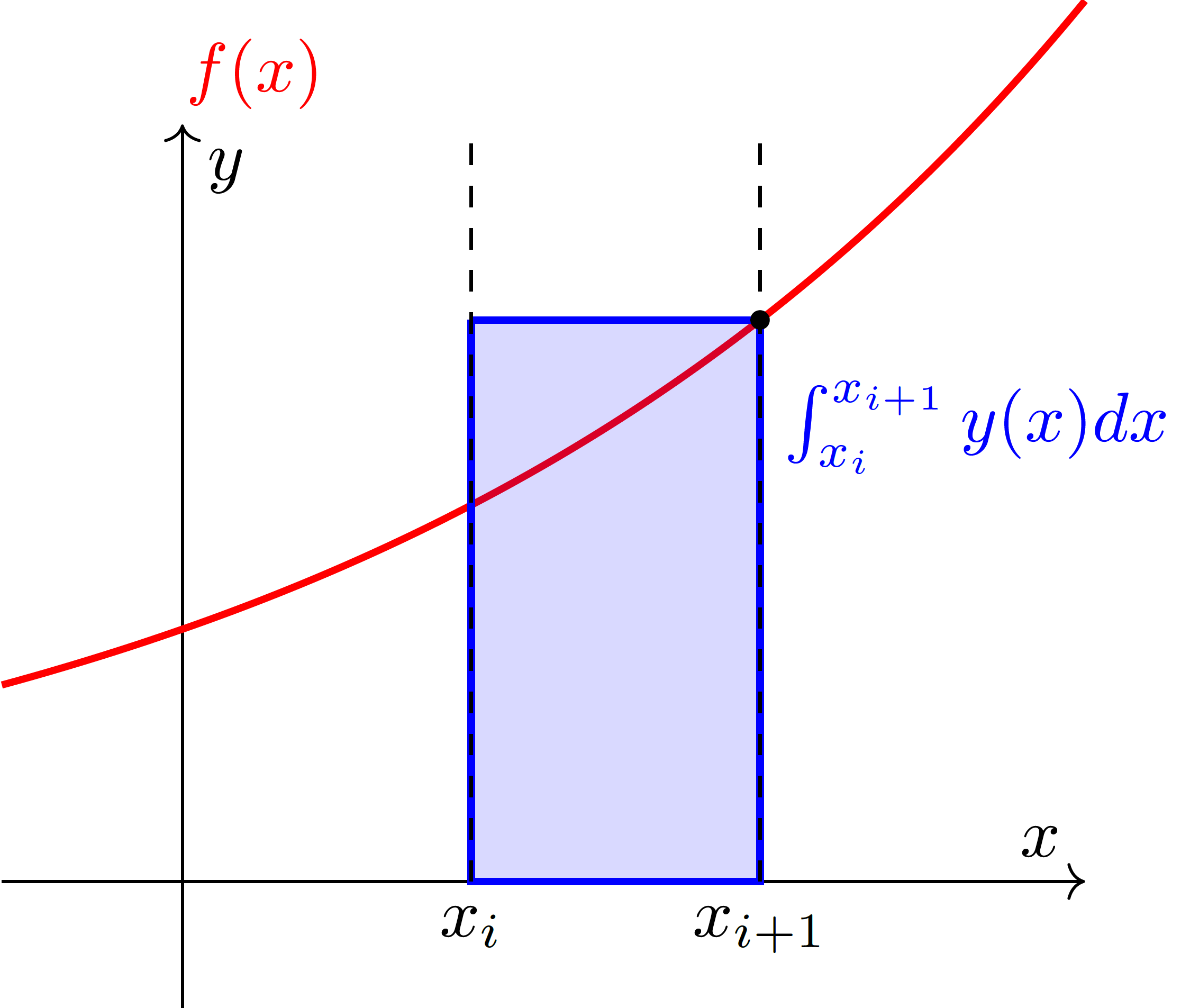
Abbildung 1: Integral einer bekannten Funktion mit der rechten Rechteckregel.

Und für die Integration einer Funktion \(f(x,y)=y'\):

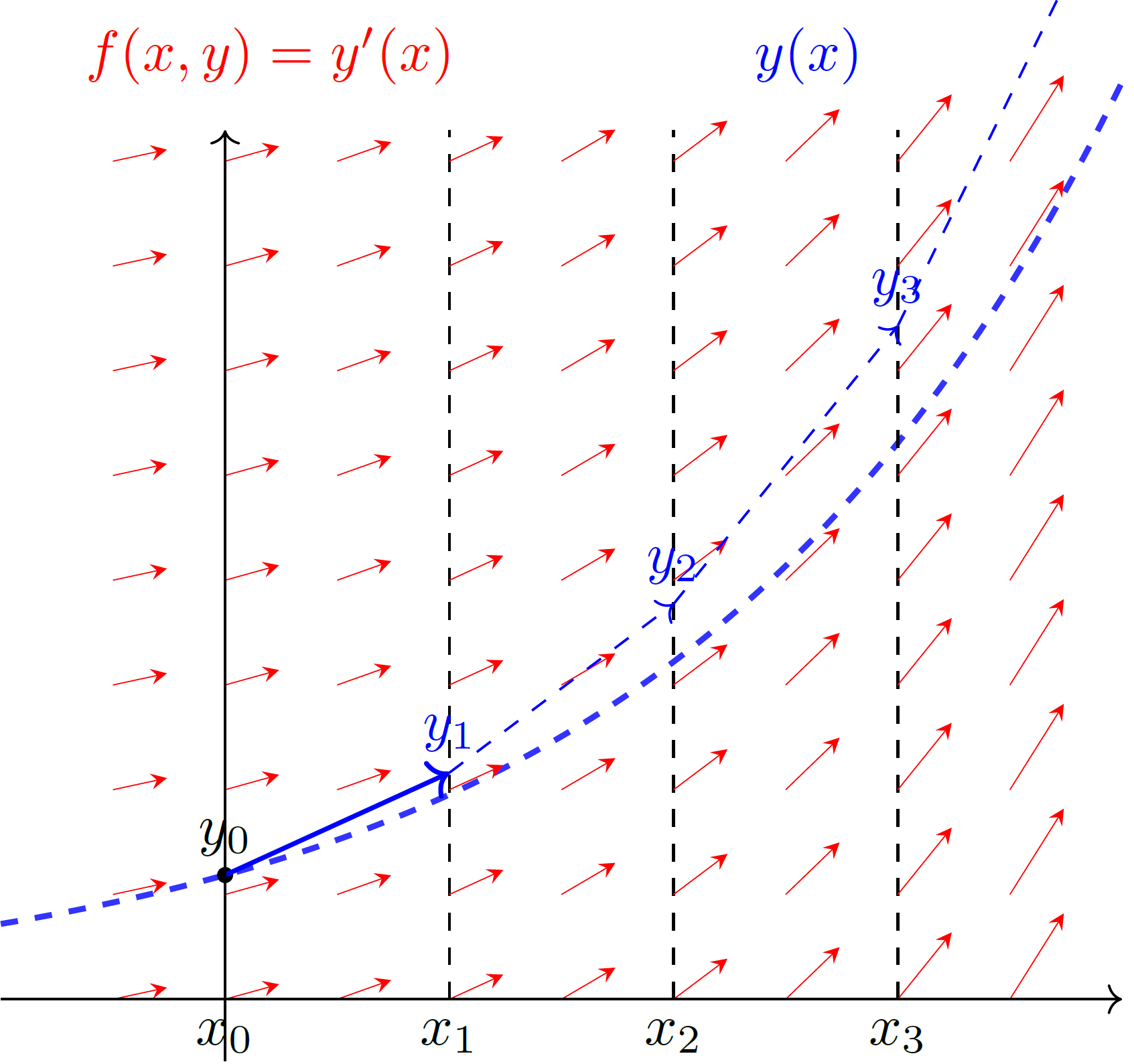
Abbildung 2: Integration einer Differentialgleichung mit der rechten Rechteckregel. Das Vektorfeld (rote Pfeile), das die Differentialgleichung an beliebigen Punkten \((x,y)\) beschreibt, wird immer am rechten Rand des diskretisierten Intervalls (\(x_1, x_2, ...\)) ausgewertet, um auf den nächsten Startwert zu schließen (blaue Pfeile). Dabei wird hier die ideale Lösung (blau gestrichelt) überschätzt.

Butcher-Tableau

\(\begin{array} {c|c} 1&1\\ \hline & 1 \end{array}\)

Hier kommt zum ersten Mal eine 1 oben links vor. Diese bedeutet, dass bereits \(K_1\) von der Stelle \(x_i + 1 \cdot h\) ausgeht. Außerdem steht zum ersten Mal in der oberen Zeile eine zusätzliche 1. Diese bedeutet, dass auch die “Schätzung” für \(y\) in \(K_1\) von \(y_i + 1 \cdot h \cdot K_1\) ausgeht.

Implementieren Sie das implizite Eulerverfahren für die Traktrix.

Tipp

Eine Matlab-Routine zum Finden von Nullstellen, nämlich fzero, kennen Sie bereits aus Newton-Verfahren. Dafür müssen Sie aus Ihrem function handle für \(g(x_i,x_{i+1})\) ein spezifisches function handle \(\~g(x_{i+1})\) definieren.

% your code here
y0    = 1;
n     = 20; % number of timesteps
tmax  = 10;
tspan = linspace(0,tmax,n);
h     = tmax/(n-1);
g     = @(yip1,yi) -yip1 + yi + h*...;
y     = zeros(n);
y(1)  = y0;
for i = 2:n
    t    = tspan(i);
    y(i) = fzero(@(yip1) g(yip1,y(i-1)));
end

plot(tspan,y)

Aufgabe 2: Die bessere Trapezregel (implizit gelöst)¶

In der Aufgabe 2: Mittelpunktsregel haben Sie die linke Rechteckregel genutzt, um Ihre Werte für die Stützstelle der Mittelpunktsregel zu schätzen, und sind bei einem Runge-Kutta-Verfahren 2. Ordnung gelandet. Lösen Sie nun die Trapezregel, bei der Sie den Funktionswert am rechten Rand des Intervalls wie oben implizit lösen.

Hinweis

Zur Erinnerung die Trapezregel:

\[\int_{x_i}^{x_{i+1}}f(x,y(x))dx \approx \frac{1}{2}h \cdot \left(f(x_i,y_i) + f(x_{i+1},y_{i+1})\right)\]

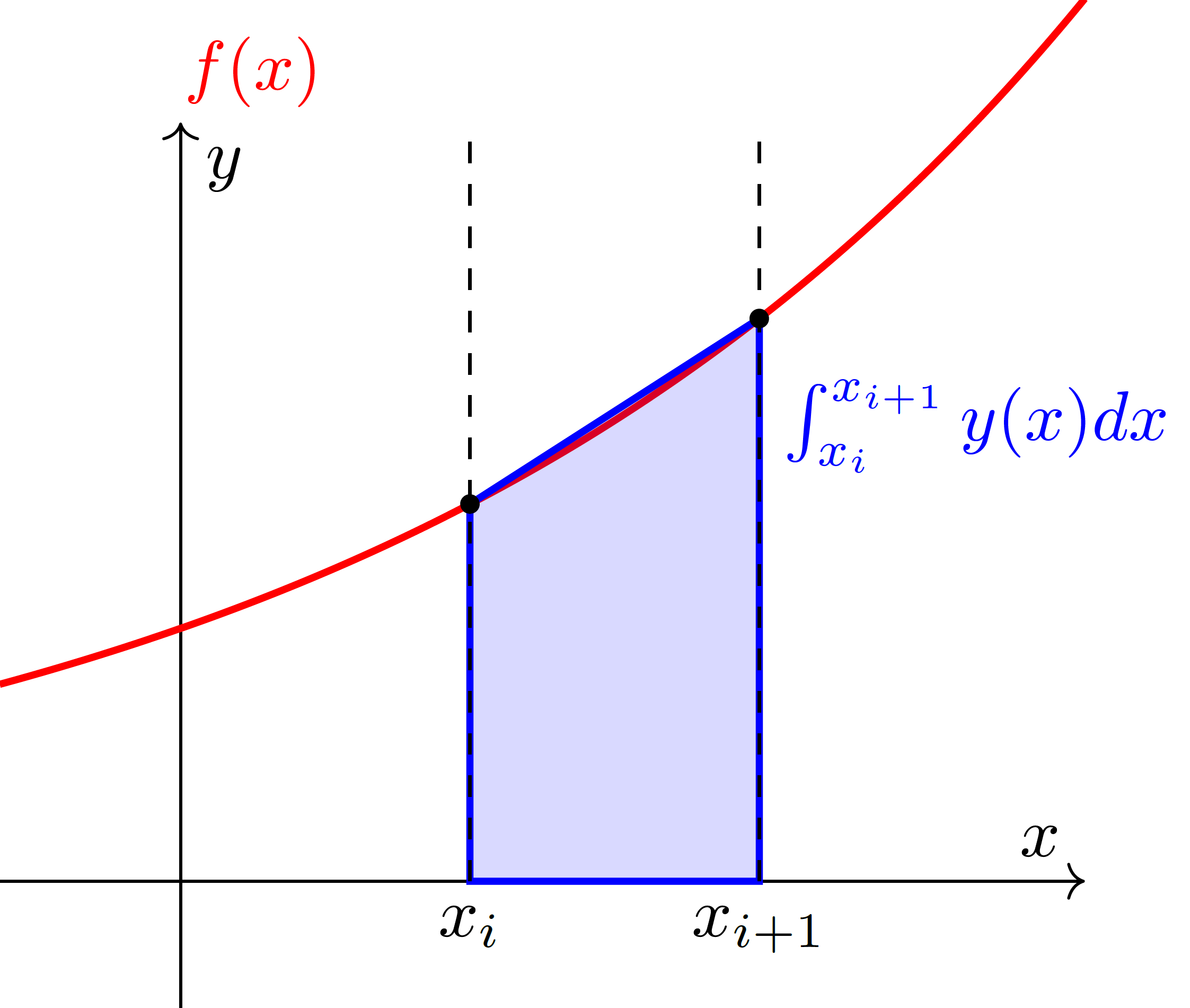
Abbildung 3: Integral einer bekannten Funktion mit der Trapezregel.

Butcher-Tableau

\(\begin{array} {c|cc} 0\\ 1&\frac{1}{2}&\frac{1}{2}\\ \hline & \frac{1}{2} & \frac{1}{2} \end{array}\)

Anders als im impliziten Eulerverfahren ist \(K_1\) einfach \(= f(x_i + 0\cdot h,y_i + 0 \cdot h \cdot K_1)\). Allerdings fließt in \(K_2\) \(K_2\) selber ein.

\[K_2 = f(x_i + 1\cdot h,y_i + h \cdot (\frac{1}{2} \cdot K_1 + \frac{1}{2} \cdot K_2)\]

Daher muss wieder implizit gelöst werden. \(y_{i+1}\) wird dann zwischen \(K_1\) und \(K_2\) mit je der Hälfte gleich gewichtet.

Merke: Die Butcher-Tableaus impliziter Verfahren erkennt man daran, dass sie keine reine untere Dreiecksmatrizen sind.

% your code here

Modellbildung und Simulation

Integration von ODEs mit impliziten Verfahren

Contents

Integration von ODEs mit impliziten Verfahren¶

Aufgabe 1: Die rechte Rechteckregel¶

Aufgabe 2: Die bessere Trapezregel (implizit gelöst)¶