Temperatur in einem nuklearen Brennstab¶

Der Brennstab eines Nuklearreaktors ist eine brennstoffgefüllte zylindrische Hülle. Innerhalb des Zylinders und auch in der Hülle entsteht Hitze durch Kernreaktionen. Die äußere Oberfläche des Zylinders wird von fließendem Wasser auf \(T_\infty = 473\;\textrm{K}\) heruntergekühlt.

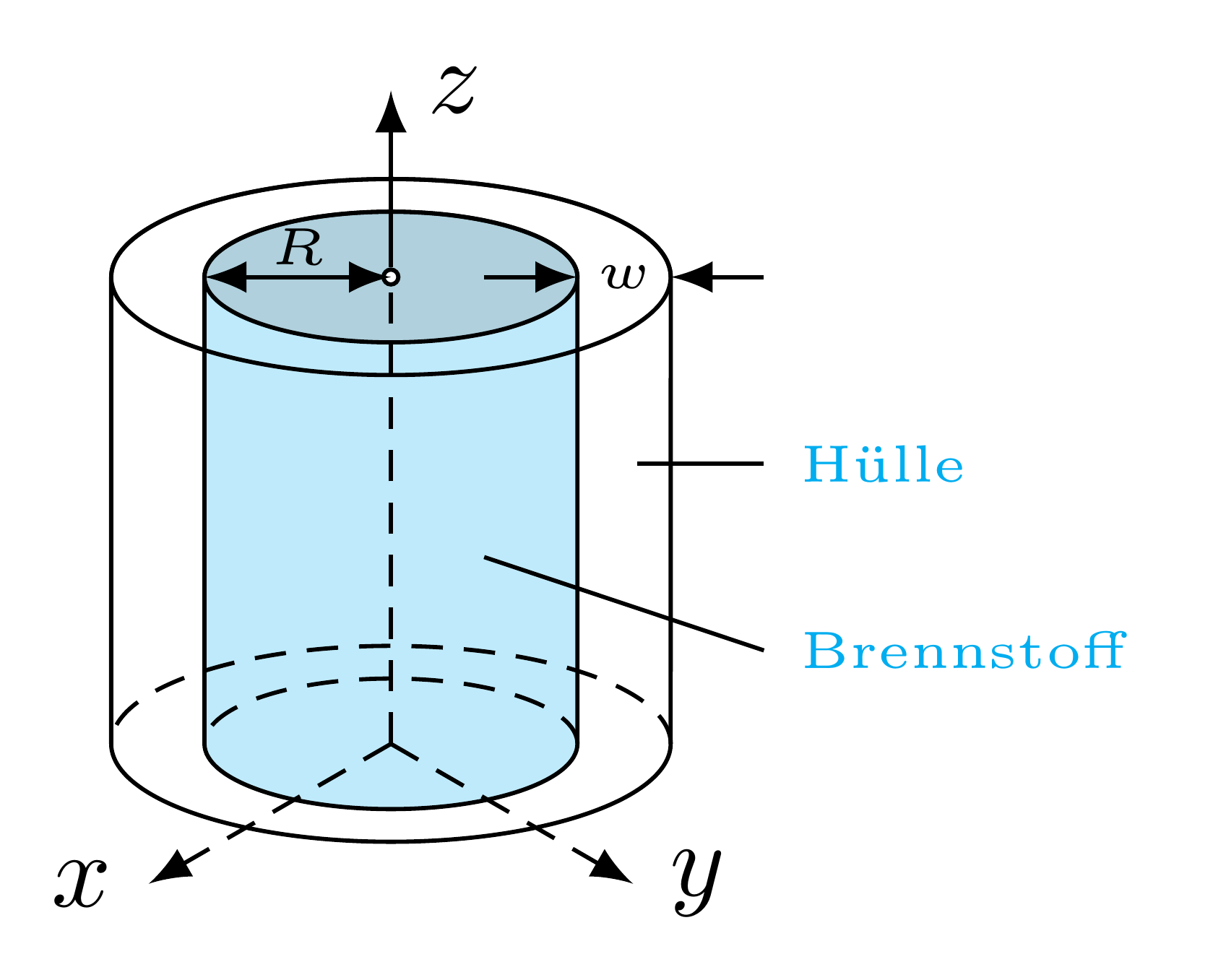
Der Wärmeübergangskoeffizient ist \(h =10^4 \; \textrm{W}/(\textrm{m}^2\mathrm{K})\). Die thermische Leitfähigkeit des Hüllenmaterials ist \(k = 16.75 \; \textrm{W}/(\textrm{mK})\). Der innere Radius des Stabes beträgt \(R=1.5 \cdot 10^{-2}\;\textrm{m}\) und die Dicke der Hülle um den Brennstab \(w = 3 \cdot 10^{-3}\;\textrm{m}\).

Konstante	Symbol	Wert	Einheit
Wärmeübergangskoeffizient	\(h\)	\(10^4\)	\(\frac{\textrm{W}}{\textrm{m}^2\textrm{K}}\)
Thermische Leitfähigkeit	\(k\)	\(16.75\)	\(\frac{\textrm{W}}{\textrm{mK}}\)
Wassertemperatur	\(T_\infty\)	\(473\)	\(\textrm{K}\)
Radius des Stabes	\(R\)	\(1.5 \cdot 10^{-2}\)	\(\textrm{m}\)
Hülle des Stabes	\(w\)	\(3 \cdot 10^{-3}\)	\(\textrm{m}\)

Die Temperaturverteilung in der Hülle kann durch Lösen der folgenden Differentialgleichung beschrieben werden:

\[ \frac{\mathrm{d}}{\mathrm{d}r} \left( r k \frac{\mathrm{d}T}{\mathrm{d}r} \right) = -10^8 \cdot e^{-\frac{r}{R}} \]

für \(R \leq r \leq R + w\). Die Randbedingungen sind

\[\begin{split} \begin{align} &\frac{\mathrm{d}T}{\mathrm{d}r}(r=R) = - \frac{6.32 \cdot 10^5 \mathrm{W}\mathrm{m}^{-2}}{k} \notag \\ &\frac{\mathrm{d}T}{\mathrm{d}r}(r=R+w) = - \frac{h}{k}(T(r=R+w) - T_\infty) \notag \end{align} \end{split}\]

Lösen Sie die Differentialgleichung mit der Matlab-Routine bvp4c.

Modellbildung und Simulation

Temperatur in einem nuklearen Brennstab

Temperatur in einem nuklearen Brennstab¶